
A livello genico esistono tre fenomeni alla base del processo che porta alla produzione delle proteine: la trascrizione, lo splicing e la traduzione. Il primo evento conduce alla sintesi di una molecola di mRNA nucleare (o trascritto primario) partendo da un filamento stampo di DNA. Successivamente l'mRNA nucleare, dopo un processo di “splicing” (ovvero il secondo fenomeno, consistente nella rimozione di sequenze di RNA introniche), migrerà dal nucleo al citoplasma, divenendo mRNA maturo (o trascritto secondario). Il terzo meccanismo è quello che, partendo da questo secondo trascritto, porterà alla sintesi della proteina finale. A livello matematico, splicing e traduzione possono venire riprodotti in ordine inverso, per dare origine (grazie all’utilizzo del codice ASCII e dell’aritmetica modulare) ad un codice crittografico simmetrico e steganografico.
SPLICING
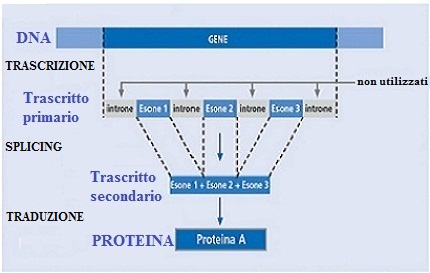
Analizzando e reinterpretando in chiave matematica i processi genici e biologici legati alla produzione delle proteine, ho creato un codice crittografico a "secret key" chiamato BERCODE. Il termine splicing (saldatura) indica uno dei processi, insieme al capping ed alla poliadenilazione, di maturazione del trascritto primario dei geni discontinui. La maggior parte degli eucarioti, nell' mRNA nucleare, presenta regioni (esoni) codificanti per proteine intervallate da altre non codificanti (introni). Dopo la trascrizione, ad opera dell’ RNA polimerasi, il trascritto primario (mRNA nucleare) va incontro a numerose modificazioni,prima fra tutte l’eliminazione degli introni, denominata splicing.
SINTESI PROTEICA
La sintesi proteica (detta anche traduzione) è il processo biochimico attraverso il quale l'informazione genetica contenuta nel mRNA maturo (successivo allo splicing e privo di introni), viene convertita in proteine che svolgono un'ampia gamma di funzioni.
ALGORITMO CRITTOGRAFICO BERCODE
Il BERCODE funziona similmente ai processi di splicing e sintesi proteica riportati sopra. Il testo in chiaro (plain text) equivale alla proteina. La criptazione consiste nel tornare dalla proteina al trascritto primario (mRNA con introni) mediante l’utilizzo di una chiave simmetrica costituita da 16 caratteri.
Il numero di esoni è stabilito dalle dimensioni del file (corrispondente ad una seconda chiave che viaggia nel testo cifrato stesso) da criptare secondo le seguenti formule:
i) Numero esoni :
- dimensione file ≤ 19 byte : n° esoni = dimensione file
- 20 byte ≤ dimensione file ≤ 99 byte : n° esoni = dimensione file/5
- 100 byte ≤ dimensione file ≤ 999 byte : n° esoni = dimensione file/10
- dimensione file ≥1000 byte : n°esoni = 5 + 541.81543 * log10(dim_file/1000) - 548.27454 * [log10(dim_file/1000)]^2 + 254.09886 * [log10(dim_file/1000)]^3 - 42.63975 * [log10(dim_file/1000)]^4
ii) Il numero di esoni, a sua volta, determina il numero dei puntatori responsabili della creazione dei caratteri intronici presenti tra un esone e l’altro:
n° puntatori = 3.377 + 90.237 * 0.962^n°esoni + codice ASCII dell’ i-esimo carattere della chiave (dove i varia, ciclicamente, da 1 a 16)
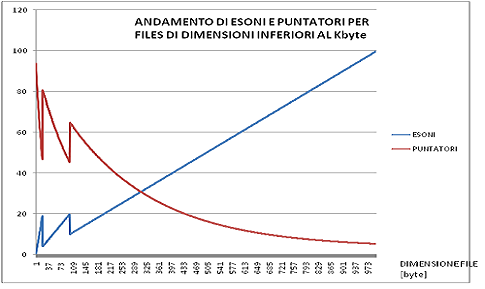
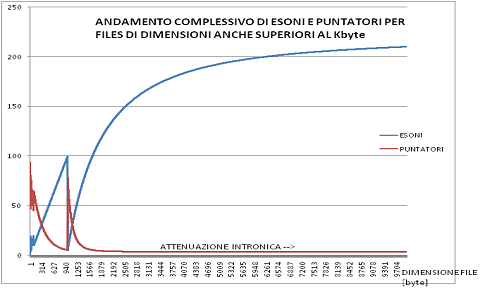
Questa formula, oltre un certo numero di esoni, presenta il fenomeno dell’attenuazione intronica, atta a limitare l’esplosione delle dimensioni del file criptato. (Per i punti i) e ii) vedere i grafici riportati più sotto);
iii) a questo punto, per creare il cipher text, genero x caratteri intronici random dove x è pari a:
x = Σ( i=1..16) codice ASCII caratterei chiave (mod 350) + 2 (somma dei codici ASCII dei caratteri della chiave (mod 350) più 2);
iv) tranne in questo unico caso, l’ultimo carattere random di ogni serie intronica che d’ora in poi verrà generata, nonchè tutti i caratteri non random, verranno criptati ed inseriti nel cipher text.
La formula di codifica viene specificata più avanti.
Dopo questa generazione di caratteri intronici, inserisco un carattere di controllo criptato per sapere se stiamo criptando un file o un testo libero; successivamente viene inserito il numero di caratteri da considerare di seguito (seguiti da un punto) e che indicano la presenza della seconda chiave (corrispondente alle dimensioni del file in chiaro);
v) adesso genero un carattere random e lo cripto posizionandolo dopo la seconda chiave. La codifica di ogni carattere in chiaro (lettera, numero, ecc…) viene effettuata modulo 256 perché ho sfruttato il codice ASCII; la formula di tale codifica è :
codice ASCII del carattere criptato = codice ASCII del carattere da criptare + codice ASCII del carattere precedente nel testo criptato + codice ASCII dell’i-esimo carattere della chiave (mod 256)
Tra un esone e l’altro (come tra la seconda chiave ed il primo esone) si inseriscono dei caratteri intronici (tutti generati in maniera casuale) ricavati mediante i seguenti passaggi:
- dopo l’ultimo esone criptato (come dopo la seconda chiave) genero un carattere random, lo cripto e lo inserisco nel cipher text. Questo è il primo puntatore. Dopo questo carattere inserisco un numero di caratteri intronici pari al codice ASCII del puntatore in chiaro;
- l’ultimo carattere di questi caratteri intronici random corrisponde al secondo puntatore e lo cripto con la solita formula del punto v). Dopo questo carattere inserisco un numero di caratteri intronici pari al codice ASCII del secondo puntatore in chiaro;
- ripeto i punti 1) e 2) per un numero di volte pari al numero di puntatori ricavato con la formula del punto ii) e poi inserisco l’esone successivo (dopo averlo criptato).
I punti 1), 2), 3) si ripetono un numero di volte pari al numero di esoni (ricavato al punto i) e continuando ad usare la chiave in modo ciclico;
vi) alla fine dell’ultimo esone genero un carattere random, lo cripto ed aggiungo un numero di caratteri intronici pari a:
codice ASCII carattere random in chiaro + codice ASCII carattere i-esimo chiave
vii) la decodifica avviene ripercorrendo tutti i punti da i) a v) ed applicando la formula di decriptazione:
carattere da criptare (in codice ASCII) = 512 + codice ASCII carattere criptato nel cipher text - codice ASCII carattere precedente nel cipher text – codice ASCII i-esimo carattere chiave (mod 256)
Come si può notare, grazie al processo di criptazione BERCODE (che è al contempo un algoritmo steganografico, ovvero di occultamento dell'informazione, ed un algoritmo crittografico), pur mantenendo invariati sia il file da cifrare sia la chiave simmetrica, il testo cifrato muta ogni volta che applichiamo l’algoritmo il che lo rende un cifratore perpetuo.
I vantaggi del BERCODE sono essenzialmente tre. Il primo è rappresentato dal fatto che lo stesso messaggio in chiaro viene codificato in modalità diversa anche usando la stessa chiave segreta il che fa sì che un'analisi delle frequenze del testo cifrato risulti vana sia all’interno del singolo cipher text sia confrontando cipher text diversi, fornendo così un vantaggio proprio solo di un sistema di crittografia "one pad". Il secondo vantaggio è rappresentato dalla velocità di codifica e di decodifica, mentre il terzo consiste nel fatto che il sistema è in grado di criptare files di qualunque tipo e dimensione.
Esempio:
Le formule di codifica e decodifica da tenere presenti durante la descrizione dell’esempio seguente sono:
Formula di codifica :
codice ASCII del carattere criptato = codice ASCII del carattere da criptare + codice ASCII del carattere precedente nel testo criptato + codice ASCII dell’i-esimo carattere della chiave (mod 256);
Formula di decodifica :
carattere da criptare (in codice ASCII) = 512 + codice ASCII carattere criptato nel cipher text - codice ASCII carattere precedente nel cipher text – codice ASCII i-esimo carattere chiave (mod 256)
A) CODIFICA
Voglio criptare il testo in chiaro “casa” e la mia chiave simmetrica è : “rternnne44gh6uhg”
1) Il testo è lungo 4 byte (quindi 4 è la mia seconda chiave che viaggia nel testo cifrato). Secondo le formule per il calcolo del numero degli esoni :
dimensione file ≤ 19 byte à n° esoni = dimensione file (in questo caso = 4)
20 byte ≤ dimensione file ≤ 99 byte à n° esoni = dimensione file/5
100 byte ≤ dimensione file ≤ 999 byte à n° esoni = dimensione file/10
n°esoni = 5+541.81543*log10(dim_file/1000)-548.27454*[log10(dim_file/1000)]2+254.09886*[log10(dim_file/1000)]3-42.63975*[log10(dim_file/1000)]4àdimensione file ≥1000 byte
e per il calcolo del numero dei puntatori (responsabili della creazione delle sequenze introniche) :
n° puntatori = 3.377+90.237*0.962(n°esoni = 4) + codice ASCII dell’ i-esimo carattere della chiave (dove i varia, ciclicamente, da 1 a 16)
con 4 byte avrò 4 esoni ed un numero di puntatori variabile tra 81 e 336
2) A questo punto, per creare il cipher text, genero x caratteri intronici random dove x è pari a:
x = Σ i=116 codice ASCII caratterei chiave (mod 350) + 2;
(somma dei codici ASCII dei caratteri della chiave (mod 350) più 2: in questo caso otteniamo 29)
Passo 1: per creare il testo criptato cominciamo, quindi, con il creare 29 caratteri random:
w^jsì463ygf351£%”()/Gfsrwòàè+
Passo 2: ora, dopo il 29° carattere random, inserisco un carattere di controllo criptato per sapere se stiamo criptando un file (carattere “f”) o un testo libero (carattere “l”). Nel nostro caso è un testo libero quindi inseriamo il carattere “l” il cui codice ASCII è 108. Per cifrare la “l” (ricordando che la chiave simmetrica è rternnne44gh6uhg) applichiamo la formula di codifica:
codice ASCII del carattere criptato = codice ASCII del carattere da criptare + codice ASCII del carattere precedente nel testo criptato + codice ASCII dell’i-esimo carattere della chiave (mod 256);
108 + 43 + 114 (mod 256) = 9
Il codice ASCII 9 corrisponde al carattere TAB (ovvero: ) quindi inseriremo questo carattere subito dopo la sequenza intronica di 29 caratteri:
w^jsì463ygf351£%”()/Gfsrwòàè+o
Passo 3: successivamente viene inserito il numero di caratteri da considerare di seguito (seguiti poi da un punto) che corrispondono alla seconda chiave (dimensioni del file in chiaro).
Nel nostro caso il numero di caratteri da considerare è 1 (in quanto la lunghezza del file dal criptare è 4 byte) quindi inseriamo il carattere “1” (il cui codice ASCII è 49) criptandolo (ricordando che la chiave segreta è rternnne44gh6uhg e di cui adesso consideriamo la t perché, per cifrare, cicliamo lungo la chiave):
49 + 9 + 116 (mod 256) = 174
Il codice ASCII 174 corrisponde al carattere “®” e quindi questo carattere verrà inserito dopo il carattere “o”:
w^jsì463ygf351£%”()/Gfsrwòàè+o®
Passo 4: a questo punto bisogna inserire il carattere “.” (punto, il cui codice ASCII è 46) cifrandolo (la chiave segreta è rternnne44gh6uhg):
46 + 174 + 101 (mod 256) = 65
Il codice ASCII 65 corrisponde al carattere “A” e quindi questo carattere verrà inserito dopo il carattere “®”:
w^jsì463ygf351£%”()/Gfsrwòàè+o®A
Passo 5: infine inseriamo la lunghezza in byte del nostro plain text : il carattere “4”. A questo carattere corrisponde il codice ASCII 52. (chiave segreta è rternnne44gh6uhg):
52 + 65 + 114 (mod 256) = 231
Il codice ASCII 231 corrisponde al carattere “ç” e quindi questo carattere verrà inserito dopo il carattere “A”:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Aç
Riepilogando:
PASSO 1 : generazione di x caratteri random (in questo caso 29) generati sommando insieme i codici ASCII di tutti i caratteri della chiave (mod 350) + 2 (x = Σ i=116 codice ASCII caratterei chiave (mod 350) + 2):
w^jsì463ygf351£%”()/Gfsrwòàè+
PASSO 2 : dopo il 29° carattere random, inserisco il carattere di controllo criptato “l” per sapere che stiamo criptando un testo libero:
w^jsì463ygf351£%”()/Gfsrwòàè+o
PASSO 3 : viene inserito il numero , criptato, di caratteri (in questo caso 1) da considerare di seguito (seguiti poi da un punto) che corrispondono alla seconda chiave (dimensioni del file in chiaro).
w^jsì463ygf351£%”()/Gfsrwòàè+o®
PASSO 4 : viene in inserito il carattere “.” (criptato) :
w^jsì463ygf351£%”()/Gfsrwòàè+o®A
PASSO 5: inseriamo la lunghezza in byte del nostro plain text : il carattere “4”.
w^jsì463ygf351£%”()/Gfsrwòàè+o®Aç
La sequenza “o®Aç” corrisponde alla seconda chiave che viaggia nel testo.
A questo punto inizia la criptazione del testo vera e propria.
Dalle formule viste sopra, sappiamo che per un file in chiaro come il nostro di 4 byte (ovvero “casa”) avremo 4 esoni, infatti:
dimensione file ≤ 19 byte à n° esoni = dimensione file (in questo caso = 4)
Sappiamo anche che con 4 esoni avremo un numero di puntatori variabile tra 81 e 336.
La chiave che usiamo per cifrare ciclicamente è rternnne44gh6uhg e siamo giunti ad utilizzare il carattere r.
Ora, dopo la sequenza iniziale nel cipher text (ovvero: w^jsì463ygf351£%”()/Gfsrwòàè+o®Aç) contenente i 29 caratteri intronici e la seconda chiave criptata, cominciamo ad inserire i puntatori atti alla generazione delle sequenze introniche.
Passo 6: Ora, dobbiamo sapere quanti puntatori generare prima di inserire il carattere “c” di casa. Il numero di puntatori, in questo caso sapendo che ciclando sulla chiave siamo giunti al carattere “n”( rternnne44gh6uhg il cui codice ASCII è 110) è:
n° puntatori = 81 + 110 = 191
Generiamo, ora, il primo dei 191 puntatori generando un carattere random, esempio “§“ (codice ASCII 167 questo vuol dire che genereremo 167 caratteri random per giungere al secondo puntatore). Adesso dobbiamo criptare il carattere “§“ sapendo che, usando la chiave simmetrica in modo ciclico, siamo arrivati al carattere “n” (rternnne44gh6uhg) e che Il cipher text attualmente è:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Aç
Quindi:
167 + 231 + carattere “ü”. Ora il testoà110 (mod 256) = 252 cifrato diventa:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü
Abbiamo detto che questo ultimo carattere corrisponde al numero (167 criptato) di caratteri random da aggiungere prima di giungere al secondo puntatore, quindi avremo un cipher text che diviene:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü….167 caratteri random..
Ora, immaginiamo che il 167° carattere random sia il carattere“\”:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü…………...\
Questo carattere viene criptato (quindi la sequenza diviene, per esempio, w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü…………...#) ed è il secondo dei 191 puntatori e ripetiamo lo stesso procedimento usato per il primo puntatore. Questo processo lo applicheremo per tutti i 191 puntatori. Otteniamo così la sequenza intronica che precede il primo esone: la “c” di casa.
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü…………......................’
Criptiamo la “c” e la inseriamo nel cipher text (per quanto riguarda l’uso ciclico della chiave simmetrica ipotizziamo di essere giunti alla “h” rternnne44gh6uhg)
99 + 39 + carattere “ò”. Ora il testoà104 (mod 256) = 242 cifrato diventa:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü…………......................’ò
Passo 7: ora dobbiamo calcolare quanti puntatori generare prima di inserire il carattere “a” di casa.
Il numero di puntatori, in questo caso sapendo che ciclando sulla chiave siamo giunti al carattere “g”( rternnne44gh6uhg il cui codice ASCII è 103) è:
n° puntatori = 81 + 103 = 184
Ripeto tutto ciò che è stato fatto al Passo 6 e poi cripto la “a” e la inserisco. Stesso discorso vale poi per la “s” (Passo 8) e la “a” (Passo 9) di casa.
Passo 10: Alla fine dell’ultimo esone genero un carattere random, lo cripto e di seguito aggiungo un numero di caratteri intronici pari a:
numero di caratteri intronici finali = codice ASCII carattere random in chiaro + codice ASCII carattere i-esimo chiave
B) DECODIFICA
In decodifica abbiamo la stessa chiave simmetrica rternnne44gh6uhg ed il testo criptato:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü.zmz,m>çmoèmbèmèpè1412302375fvklvasooj’j’j’0jweqnlalqisbbgsdqwz43udc7/&”=$%%!/)£JDLçòxlòlòsb°°ç駰è*YDHHISH82698)()£&%&$^^?Péç°°:_JSUISIOSOSOHBCCjb--.,…………......................
Passo 1: dobbiamo ricavare l’informazione relativa al tipo ed alla lunghezza del file. Sommiamo, allora, tutti i codici ASCII dei caratteri della chiave e gli aggiungiamo 2 ed otteniamo 29:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü.zmz,m>çmoèmbèmèpè1412302375fvklvasooj’j’j’0jweqnlalqisbbgsdqwz43udc7/&”=$%%!/)£JDLçòxlòlòsb°°ç駰è*YDHHISH82698)()£&%&$^^?Péç°°:_JSUISIOSOSOHBCCjb--.…………......................
Passo 2: Questi 29 caratteri corrispondono alla prima sequenza intronica. Il carattere successivo indica se il testo che stiamo criptando è un file (“f”) o un testo libero (“l”).
Decodifichiamo il carattere successivo TAB “o” (codice ASCII : 9) con la formula di decodifica, iniziando a ciclare sulla chiave rternnne44gh6uhg:
carattere da criptare (in codice ASCII) = 512 + codice ASCII carattere criptato nel cipher text - codice ASCII carattere precedente nel cipher text – codice ASCII i-esimo carattere chiave (mod 256)
Nel nostro caso:
carattere da criptare (in codice ASCII) = 512 + 9 – 43 – 114 (mod 256) = 108 (corrispondente al carattere “l”)
Sappiamo quindi che il testo è un testo libero.
Passo 3: Dobbiamo ora sapere la dimensione del file. Per ottenere questa informazione dobbiamo decriptare il carattere “®”. (Chiave simmetrica: rternnne44gh6uhg)
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü.zmz…………
carattere da criptare (in codice ASCII) = 512 + 174 – 9 – 116 (mod 256) = 49 (corrispondente al carattere “1”).
Continuiamo a decriptare w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü.zmz………… (Chiave simmetrica: rternnne44gh6uhg):
carattere da criptare (in codice ASCII) = 512 + 65 – 174 – 101 (mod 256) = 46 (corrispondente al carattere “.”).
Abbiamo individuato il carattere “.”, il che, insieme al carattere “1” decriptato prima, ci dice che le dimensioni del file saranno comprese tra 1 e 9 byte.
Continuiamo a decriptare w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü.zmz………… (Chiave simmetrica: rternnne44gh6uhg):
carattere da criptare (in codice ASCII) = 512 + 231 – 65 – 114 (mod 256) = 52 (corrispondente al carattere “4”).
Abbiamo recuperato, adesso, tutte le informazioni riguardanti il file in chiaro: è un testo libero di 4 byte di memoria. Ci ricaviamo allora:
- àdimensione file ≤ 19 byte n° esoni = dimensione file (in questo caso = 4)
- n° puntatori = 3.377+90.237*0.962(n°esoni = 4) + codice ASCII dell’ i-esimo carattere della chiave (dove i varia, ciclicamente, da 1 a 16) in questo caso con 4 byte avrò 4 esoni ed un numero di puntatori variabile tra 81 e 336.
Passo 4: Ora, dobbiamo sapere quanti puntatori sono stati generati prima di inserire il primo carattere nel file cifrato. Il numero di puntatori, in questo caso sapendo che ciclando sulla chiave siamo giunti al carattere “n”(rternnne44gh6uhg il cui codice ASCII è 110), è:
n° puntatori = 81 + 110 = 191
Il primo dei 191 puntatori è quello criptato ed inserito nel testo cifrato subito dopo la seconda chiave:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü……………………………………..
codice ASCII = 252)àPer sapere quanti caratteri calcolare prima di giungere al secondo dei 191 puntatori decripto questo carattere (ü
carattere da criptare (in codice ASCII) = 512 + 252 – 231 – 110 (mod 256) = 167 (corrispondente al carattere “§”). Questo vuol dire che il secondo dei 191 puntatori si troverà dopo 167 caratteri random.
Ripeto questo processo per gli altri 189 puntatori per poi giungere al primo carattere del cipher text da decriptare:
w^jsì463ygf351£%”()/Gfsrwòàè+o®Açü…………......................’ò
Il carattere “ò” è quello individuato dal 191° puntatore e quindi sappiamo che corrisponde al nostro primo carattere del testo cifrato e quindi lo decifriamo con la formula legata alla chiave rternnne44gh6uhg (dove ciclando siamo giunti, per esempio, al carattere “h”):
carattere da criptare (in codice ASCII) = 512 + 242 – 39 – 104 (mod 256) = 99 (corrispondente al carattere “c”). Abbiamo così trovato e decifrato il primo carattere del nostro testo in chiaro.
Passo 5: Ora dobbiamo calcolare il numero di puntatori che ci separano dal secondo carattere (“a”) (esone) del nostro plain text, e lo calcoliamo mediante la formula, sapendo che ciclando sulla chiave simmetrica siamo giunti al carattere “g” (codice ASCII: 103) rternnne44gh6uhg :
n° puntatori = 81 + 103=184
Il 184° puntatore individuerà il secondo carattere da decriptare, e ripeterò questi processi per il terzo (Passo 6) (“s”) e per il quarto carattere (“a”) (Passo 7) del mio testo in chiaro, giungendo alla completa decodifica del testo cifrato.
Daniele Bertaggia


Immagino tu ti riferisca alla seconda parte dell’articolo (in quanto la prima è chiara e ben leggibile).
Della formattazione si sono occupati Piero (content manager) e Daniele (l’autore) ed io l’ho approvata.
Sinceramente non mi aveva molto soddisfatto la formattazione della seconda parte dell’articolo ma ho lasciato correre perché l’ho trovata in linea con l’argomento trattato. Fermo restando che la prima parte è ben chiara, la seconda è…ermetica!
Per carità è solo un mio pensiero, sentiamo anche le giustificazioni di Piero e Daniele 🙂
Utilizzare quanto presente in natura per migliorare la sicurezza della crittografia mi sembra una soluzione molto intelligente, sfruttare poi il DNA e la genetica, credo sia davvero un’ottima intuizione!
A livello pratico si dovrebbe applicare tale sistema ai sistemi di scambio dati per poterne testare a fondo la sicurezza. Magari integrandolo in un algoritmo compatibile con i sistemi embedded.
Riguardo invece l’affidabilità e la sicurezza della genetica (ed i suoi misteri) mi piacerebbe sentire dei pareri autorevoli. Ci vorrebbe un matematico e… un filosofo! (fortunatamente ci leggono entrambi)
Ciao Emanuele,
ti ringrazio per i tuoi apprezzamenti. Piacerebbe molto anche a me sviluppare ulteriormente l’argomento; magari scopriremmo che la genetica ha in serbo altri fenomeni che potrebbero risultare utili anche in altri campi. D’altronde miliardi di anni di evoluzione vorranno pur dire qualche cosa….
Ciao a tutti. Su richiesta di Emanuele avevo sviluppato un esempio concreto in Word (usando diversi colori per rendere più comprensibile l’esempio stesso). Successivamente Emanuele mi aveva detto di inserirlo direttamente nell’articolo, tralasciando il documento di Word. Nell’inserirlo direttamente nell’articolo tutti i colori ed i vari accorgimenti sono andati persi con il conseguente risultato. Ora capisco anche perché Emanuele l’ha voluta mantenere ugualmente.
Sapendo ben poco sia di crittografia che di genetica, ritengo che il mio parere sia tutt’altro che autorevole. Posso solo dire che, siccome molte delle invenzioni dell’uomo sono state una sorta di imitazione di qualcosa che era già presente in natura (ad es., il sonar dei pipistrelli), non mi meraviglierei affatto se questa originale idea di realizzare un codice crittografico ispirandosi alla genetica si rivelasse proficua.
Anche perchè la genetica funziona, a differenza di tutto ciò che di artificiale esiste che ha bisogno di veriche, collaudi, correzioni, revisioni ed occasionali riparazioni 🙂
Onestamente? Io non ricordo che fosse questa la resa grafica che ho approvato…!
In bozza c’erano spazi ed andate a capo che non saprei dire perchè non ci sono più ora!!
Ci tengo a dire che ritengo semplicemente inaccettabile il modo in cui questo articolo è visibile oggi e domando scusa a tutti i lettori perchè il mio lavoro di revisione è stato palesemente e rovinosamente insoddisfacente!
Si, lo penso anche io.
È l’unica ragione che mi venga in mente.
Non sono, purtroppo, però, in grado di immaginarne il motivo!
Il ragionamento secondo cui un algoritmo crittografico asimmetrico è sempre preferibile ad un algoritmo crittografico simmetrico non è scontato. Un algoritmo asimmetrico è affidabile ma lento. Il tempo che serve al messaggio per essere codificato e decodificato è relativamente alto. Questo è il principale svantaggio della decodifica asimmetrica. (Tra l’altro un codice simmetrico può essere usato anche in maniera asimmetrica….).
Per compensare i reciproci svantaggi (lentezza asimmetrica, problema distribuzioni chiavi simmetrica) esistono procedure ibride che riassumono le caratteristiche dei due tipi di crittografia. Ad esempio può venire usato contemporaneamente sia un algoritmo a chiave simmetrica sia uno a chiave asimmetrica. Ogni utente ha una coppia di chiavi privata e pubblica. Ogni volta che il mittente apre una nuova sessione il sistema genera una chiave simmetrica di sessione che viene criptata con la chiave pubblica del destinatario, e spedita con il messaggio. Il destinatario decripta la chiave di sessione attraverso la sua chiave privata, quindi asimmetrica, ed infine usa la chiave di sessione, simmetrica, per decodificare il messaggio. Abbiamo così unito la comodità nella gestione delle chiavi del sistema asimmetrico con la velocità propria di quello simmetrico.
Tornando al Bercode:
1) Usato in maniera asimmetrica aggiungerebbe il vantaggio della cifratura perpetua;
2) Unito ad esempio all’uso dell’ RSA, aggiunge il vantaggio della velocità simmetrica;
3) Valore epistemologico legato allo studio di dinamiche interne ad un ambito (esempio scrutare dinamiche e processi metabolici cellulari) e trasferirli in un ambito totalmente diverso (esempio l’ambito matematico della crittografia)
Ho fatto l’esempio dell’RSA perché è il primo algoritmo asimmetrico che mi è venuto in mente (forse perché uno dei suoi tre inventori, ovvero Adleman, era un biologo molecolare…)
Volevo fare l’esempio di un codice asimmetrico anche se, in realtà, l’RSA presenta gli svantaggi tipici dei codici crittografici asimmetrici, nel senso che:
1) è sensibile ad attacchi del tipo chosen plain-text;
2)la mole dei calcoli aritmetici in campo, per numeri grandi, si traduce in una lentezza della codifica. Anche così RSA resta un metodo di cifratura molto più lento (circa mille volte) degli algoritmi classici come DES; per questo motivo RSA è di solito utilizzato solo per trasmettere la chiave segreta di un AES (o altro cifrario simmetrico) e il messaggio vero e proprio viene trasmesso appunto con il AES (o altro cifrario simmetrico).
Quindi con RSA intendo un codice asimmetrico in genere…