
Ogni tanto, tutti ci sentiamo di sognare di viaggiare nel tempo. Non sarebbe meraviglioso ritornare in quel punto specifico del passato per cambiare una decisione negativa o rivivere un'esperienza. O addirittura andare nel futuro per studiare cosa ci aspetta.
È possibile costruire una macchina del tempo che trasporterà un essere umano nel passato o nel futuro? Per decenni, il viaggio del tempo è stato concepito come un qualcosa fantascientifico. Negli ultimi anni, tuttavia, l'argomento è diventato un settore di studio tra i fisici teorici. La comprensione della relazione tra causa ed effetto è una parte fondamentale dei tentativi di costruire una teoria unitaria della fisica. Se fosse possibile un viaggio illimitato, anche in linea di principio, la natura di una tale teoria unificata potrebbe essere drasticamente colpita. La nostra migliore comprensione del tempo deriva dalle teorie della relatività di Einstein. Prima di queste, il tempo è stato ampiamente considerato assoluto e universale, ovvero lo stesso per tutti. Nel 1948 Kurt Gödel produsse una soluzione delle equazioni di campo gravitazionale di Einstein che descrivevano un universo rotante. In questo universo, un astronauta potrebbe viaggiare attraverso lo spazio per raggiungere il proprio passato. Ciò è dovuto al modo in cui la gravità influenza la luce. La rotazione dell'universo trascinerebbe la luce (e quindi le relazioni causali tra gli oggetti) attorno ad essa, consentendo a un oggetto materiale di viaggiare in un anello chiuso nello spazio, senza che in qualsiasi fase superi la velocità di luce nell'immediato vicinato della particella.
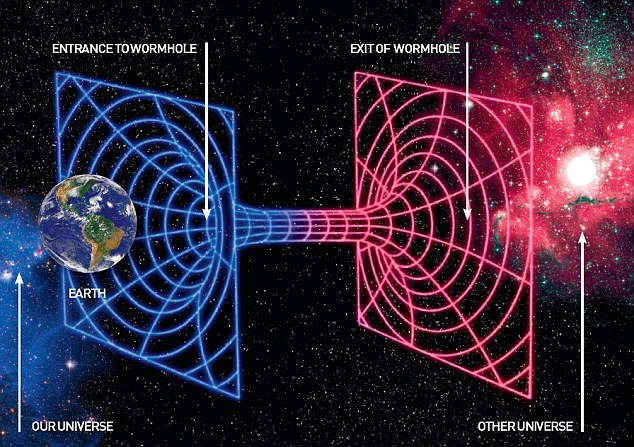
Con il passare degli anni si sono susseguite varie teorie, l'ultima, emersa negli anni '80, ha proposto uno scenario più realistico per una macchina del tempo, basato sul concetto di un wormhole. I wormholes appartengono naturalmente alla teoria generale della relatività, per cui la gravità non si limita solo al tempo ma anche allo spazio (figura 1).
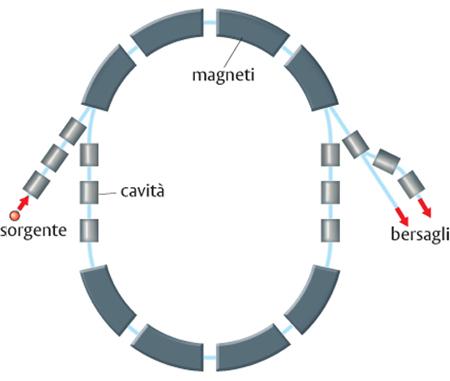
La teoria consente l'analogo di percorsi alternativi (strade e tunnel) che collegano due punti nello spazio. Un astronauta che vi passa attraverso potrebbe uscire non solo in un altro luogo dell'universo, ma anche altrove, sia nel futuro che nel passato. È concepibile che la prossima generazione di acceleratori di particelle saranno in grado di creare wormholes subatomici. Gli acceleratori di particelle impiegati nella fisica medica hanno lo scopo di incrementare l'energia cinetica delle particelle subatomiche coinvolte, con l'obiettivo di sondare proprietà della materia. Purtroppo, questi tunnel sono solo un miliardo trilioni di trilioni di centimetri. Un modo troppo piccolo per far passare un essere umano. Alcuni scienziati pensano che possa essere possibile catturare un wormhole e ingrandirlo molti trilioni di volte per renderlo abbastanza grande per un uomo o addirittura per un'astronave affinchè possa entrarci. Un acceleratore potrebbe generare energia sufficiente per creare particelle che esistono in altre dimensioni, ma può anche produrre anti-particelle, una possibile fonte per la materia oscura. Ora, l'energia può essere così concentrata affinchè anche il tessuto dello spazio-tempo possa essere distrutto per creare un wormhole, non in un luogo diverso, ma in un tempo diverso (figura 2).
Supponendo che i problemi di ingegneria possano essere superati, la realizzazione di una macchina del tempo potrebbe aprire una scatola di paradossi. Considerate, ad esempio, il viaggiatore di tempo che visita il passato e uccide sua madre. Come ci rendiamo conto di questo? Anche se il viaggio del tempo non è strettamente paradossale, è certamente strano.





Gödel regalò ad Einstein la soluzione citata nel post, in occasione del suo 70esimo compleanno.
C’è un aneddoto su Gödel: quando qualcuno gli chiedeva: “perché un universo rotante”? Gödel anzichè rispondere, guardava in alto nel cielo, e solo dopo molto tempo rispondeva domandando: “esiste nell’universo un qualche corpo celeste non rotante?” In altre parole, l’esistenza di un momento angolare di spin sembra essere un grado di libertà inerente ai corpi celesti e più in generale, all’intero universo. Inoltre, Gödel scelse ad hoc quella particolare metrica che a differenza di quella di Robertson-Walker rende impossibile la sincronizzazione degli orologi (che in RG è possibile solo in un dato sistema di riferimento)
Come detto gia’ un altro post, il fatto stesso che la GR ammetta metrica con traiettorie di tipo tempo chiuse, potrebbe essere un segnale che questo sia possibile, dove per possibile si intende ovviamente “ammesso fra le soluzioni della teoria”.
Questo rinnesca tutto il nostro discorso sull’effettiva necessita’ di una legge di Natura “causa -> effetto”. C’e’ da dire che tutt la GR, e soprattutto lo studio di topologia differenziale di Penrose-Hawking con cui “dimostrarono” il big-bang, si basa proprio sul cono degli eventi intorno a un dato punto dello spazio-tempo.
Cio’ non toglie (approccio Penrosiano al mondo della Matematica separato dalla realta’) che la GR sia solo una teoria (per quanto forse quella piu’ perfetta, elegante e verificata) e che ci siano altre teorie che ammettano la non causalita’.
E’ difficile cmq anche pensare ad esperimenti che simulimo la metrica di Goedel, cmq.
ho trovato l’articolo di Novikov su arxiv. È del 1996, e postula un principio di auto-consistenza… https://arxiv.org/pdf/gr-qc/9506087.pdf
Ottimo Marcello, veramente interessante. Provero’ a leggerlo, sperando di avere tutte le competenze per capirlo a fondo. Poi tornerò qui per commentarlo. Grazie.
Leggendo il wiki sul principio di self-consistency:
https://en.wikipedia.org/wiki/Novikov_self-consistency_principle#cite_note-Krasnikov2001pp14-16-17
fa un bell’esempio (che avevo gia’ letto sul saggi odi Thorne) di una palla da biliardo che entra in worm-hole ed esce nel passato colpendo se stessa e quindi impedendole di andare nel futuro. Questo e’ il famoso paradosso di Polchinski.
Ci son state diverse soluzioni a questo, che e’ il solito paradosso che poi si svela non esserlo (tipico di paradossi relativistici).
Nel dettaglio:
“If CTCs are allowed, and if the above vision of theoretical physics’ accommodation with them turns out to be more or less correct, then what will this imply about the philosophical notion of free will for humans and other intelligent beings? It certainly will imply that intelligent beings cannot change the past. Such change is incompatible with the principle of self-consistency”
Andando oltre a questo, si vede come tutto si appoggi pesantemente sul principio di libero arbitrio (free will) cosi’ come formulato dall’immenso John Conway (altro mio eroe che fa il paio con Penrose):
Ovvero:
“The free will theorem of John H. Conway and Simon B. Kochen states that if we have a free will in the sense that our choices are not a function of the past, then, subject to certain assumptions, so must some elementary particles” (da wikipedia).
Quindi, cosi’ un essere senziente non puo’ influenzare il passato (secondo il principio di self consistency di Novikov) cosi’ non lo puo’ una particella quantistica.
Cmq, gia’ solo sul Free Will se ne potrebbe parlare per pagine e pagine.
Proseguo col pdf.
Interessante cmq questo commento nel free will su wiki:
“The philosopher David Hodgson supports this theorem as showing determinism is unscientific, that quantum mechanics allows observers (at least in some instances) the freedom to make observations of their choosing, and so leaves the door open for free will”
Da una prima lettura sembra effettivamente derivare il principio di self-consistency dal principio di minima azione, in modo molto “semplice” (anche se lungo da seguire) poiche’ non utilizza concetti di velocità’ super-relativistiche o altri tool astrusi e complessi, bensi’ semplicemente una particella classica che entra in wormhole a un tempo t + Dt e ne esce a un tempo t. Questo tempo e’ quello valutato da un osservatore stazionario col wormhole, quindi dal suo punto di vista la particella emerge nel passato, viaggiando quindi indietro nel tempo.
La trattazione e’ veramente classica e applica il principio di minima azione, ovvero quello che rende stazionaria l’azione del sistema, ricavando l’equazioni del moto. Per i 2 tratti fuori dal wormhole, emergono esattamente le semplici equazioni del moto di Newton. Il wormhole e’ considerato avente le bocche di “massa infinita” in modo da trascurare il loro rinculo al passaggio della particella. All’interno del wormhole, e qui viene la parte tricky, hanno modellizzato la self-interaction della particella utilizzando un semplice escamotage: hanno splittato la particella in 2, facendola interagire con l’altra mediante un potenziale opportuno. Il potenziale scelto, che sembra “semplificare i calcoli” e’ il potenziale di tipo hard-shell, cioe’ quello di 2 palle da biliardo in collisione. Mi resta il dubbio del perche’ la self interaction sia stata modellizata SOLO all’interno del wormhole.
Da tutto questo, dopo N pagine, sembra appunto venir fuori che le uniche traiettorie che rendono stazionaria l’azione su tutto il tratto sia quelle ipotizzate dal principio di self-consistency di Novikov (ipotizzate in un altro articolo precedente).
Devo ancora capirlo bene, ma credo queste traiettorie siano quelle per cui sia impossibile che la particella torni indietro nel tempo per influenzare se stessa (ovvero appunto il paradosso di Polchinski). Questo modo di modellizzare splittando la particella in 2 serve appunto per ricavare i vincoli (constraint) che l’equazione devono prendere per evitare paradossi spazio temporali.
Da notare quindi, che questo principio NON VIETA le CTC o i viaggi indietro nel tempo, bensi’ forza le traiettorie in modo che un essere senziente o meno NON POSSA interagire con se stesso nel passato. Come detto, quindi, non c’e’ Free Will per i viaggi nel passato.
Quindi non va contro all’esistenza delle CTC, ma ne vieta in un certo modo la forma.
Tutti i piu’ grandi relativisti sembrano essersi occupati prima o poi delle CTC. Lo stesso Hawking:
https://en.wikipedia.org/wiki/Chronology_protection_conjecture
Consiglio cmq a tutti almeno una scorsa veloce all’articolo proposto da Marcello. E’ un splendido esempio di come i Fisici ragionino partendo da assunti che spesso sfuggono (ad esempio, assumere per semplificare che le bocche abbiano inerzia infinita, e’ un buon criterio. Io, che non sono un fisico di professione, gia’ mi farei 3000 domande prima di farlo, sulla correttezza di questo assunto). Spesso gli articoli scientifici (da fisici per i fisici) sono molto spinti e tralasciano gran parte dei dettagli. Questo, invece, benché complesso e lungo permette di seguire il ragionamento dall’inizio alla fine, con tutti i dettagli del caso.
Seguendo questo principio di Novikov, che non e’ cmq accettato universalmente, si puo’ quindi rispondere prontamente alla domanda posta nel testo del post:
“Considerate, ad esempio, il viaggiatore di tempo che visita il passato e uccide sua madre”.
Ebbene, secondo questo principio (che emerge dal principio di minima azione, universale in Fisica) NON E’ possibile che un essere senziente possa volontariamente tornare indietro nel tempo e modificare il proprio passato. Non c’e’ quindi “free will” in questo caso, ma una palla da biliardo che passi per un wormhole potra’ assumere solo delle traiettorie tali da non influenzare se stessa nel passato.
Se vogliamo, per quel che posso vedere dire, e’ una specie di “quantizzazione” delle traiettorie possibili. Anche in meccanica quantistica, ad esempio, il momento angolare puo’ assumere solo valori quantizzati e ben precisi per una data configurazione. Ecco, analogamente anche qui solo alcune CTC (curve di tipo tempo chiuse) potranno essere ammesse.
Alcuni cmq criticano questo principio, chiaramente sforando nella metafisica.
Interessante cmq la conseguenza delle CTC, dal punto di vista della teoria della computazione complessa. Sempre da:
https://en.wikipedia.org/wiki/Novikov_self-consistency_principle
Si legge sul fondo:
“Time-loop logic, coined by roboticist and futurist Hans Moravec,[11] is a hypothetical system of computation that exploits the Novikov self-consistency principle to compute answers much faster than possible with the standard model of computational complexity using Turing machines. In this system, a computer sends a result of a computation backwards through time and relies upon the self-consistency principle to force the sent result to be correct”
Il principio e’ poi stato portato oltre dal grande Deutsch, dimostrato con una simulazione:
“Deutsch shows that quantum computation with a negative delay—backwards time travel—produces only self-consistent solutions, and the chronology-violating region imposes constraints that are not apparent through classical reasoning.[12] Researchers published in 2014 a simulation validating Deutsch’s model with photons”
Chissa’ se vedremo queste cose applicate nel futuro. Anche il quantum crypting sembrava fantascienza, eppure ora e’ gia’ usato.
Nel frattempo ho trovato quello del “biliardo di Nokikov”. Era sepolto nell’hard disk dal 2000! l’ho messo online http://www.extrabyte.info/biliardo.pdf
Grazie Marcello, quest’articolo e’ ancora piu’ esaustivo dell’altro, essendo di questo una specializzazione (e venendo dopo anche in ordine di tempo).
Qui mi si conferma che il trick di splittare la particella in 2 identiche equivale, sotto certi aspetti, a simulare la self-interaction con se stessa. L’autore nel paragrafo “jinnee of Time Machine” spiega bene e in dettaglio le varie possibilita’ interpretative.
Non ho capito subito o cosa si riferisse l’autore con “Jinnee”, ho pero’ poi trovato qui la spiegazione:
https://en.wikipedia.org/wiki/Causal_loop
che illustra esattamente il problema del “biliardo di Novikov”. Sto cercando di leggerlo il piu’ attentamente possibile, anche se ci vuole tempo. In ogni caso, alla fine del tutto l’autore getta questo disclaimer per usi futuri:
“It may be supposed that correct formulation of this problem may be given only in the framework of quantum theory.”
Chissa’ se qualcuno sia mai partito da qui per una formulazione di quantum gravity?
Proprio come Feynman descrisse che tutta l’essenza della QM era catturabile nel “double slit experiment”, ho una forte sensazione che proprio questo “biliardo di Novikov”, esteso alla QM, potrebbe gettare le basi per un super-mix della tanto agognata “quantum gravity” theory.
Ne ha tutte gli ingredienti: “causalita’, GR, CTC” piu’ la parte di QM (che non ho ancora cercato in rete relazionata a questo). Se pero’ aggiugiamo la recente teoria di Sussking e Maldacena, che congetturano che ER = EPR, cioe’ l’entanglement possa essere spiegato con i wormholes, ecco che l’anello mancante del biliardo in questione con la QM appare magicamente. E’ solo una sensazione e, chiaramente, non ho le capacita’ ne le conoscenze per suffragarla.
Hai ragione: ci vuole tempo! Stavo cmq pensando di considerare un modello 1-dimensionale.
Una specie di “flatlandia” incurvata, e che quindi non sarebbe più una flatlandia.
Si parte da una particella relativistica che compie un moto unidimensionale, per cui abbiamo uno spaziotempo 2-dim, ovviamente piatto (con la solita metrica di Minkosky). Il passo successivo consiste nell’incurvare lo spaziotempo, però in una modalità del tutto astratta, cioè senza giustificare il tutto da un punto di vista fisico. Ad esempio, lo spaziotempo potrebbe essere la superficie di una sfera, per cui le coordinate sferiche (o polari) (theta, phi) svolgerebbero il ruolo di coordinate spaziotemporali. Precisamente, l’arco complementare di theta rappresenterebbe la coordinata temporale (più precisamente moltiplcando per il raggio R della sfera, si ottiene l’analogo di ct nell’usuale metrica di Minkosky). A questo punto si scrive una lagrangiana, tentando poi di tirar fuori un qualcosa di simile al principio di auto-consistenza di Novikov.
Un sistema del genere dovrebbe emulare un biliardo di Novikov 1-dim.
correggo: flatlandia è 2-dim
minkosky->minkowsy
nel caso di uno spaziotempo 2dim i conti sono di gran lunga più semplici, considerando poi il caso di una 2-sfera, per poi generalizzarli a 4-dim
OK capito quello che vuoi dire, ma ho dei dubbi sulla sfera: lo spazio tempo che vuoi modellizzare e’ Minkowsky, quindi e’ iperbolico e non sferico, da quel che ricordo. Forse quindi e’ piu’ opportuno un iperboloide (con curvatura negativa, quindi).
ho usato un abuso di linguaggio: lo spazio-tempo di Minkowsky e’ ovviamente piatto, poiche’ modellizza quello utilizzato nella relativita’ ristretta. Quello che intendevo dire e’ che, vista la segnatura della metrica dello spazio di Minkowski, una distanza fra 2 punti e’ equivalente alla distanza presa su un iperboloide, come descritto qui:
https://it.wikipedia.org/wiki/Geometria_iperbolica
“La descrizione matematica di questo modello ha forti analogie con lo spaziotempo di Minkowski: la distanza fra due punti è la stessa usata nella relatività speciale.”
Tutti gli “embedded diagrams”, anche 1-D (quindi x e t solamente) sono modellizzati da un iperboloide, ad esempio (sia nel caso Minkowski, sia nel caso semplice piu’ complesso di Black Holes).
Interessante approccio cmq. Come pensavi di realizzare la self-intersection dentro la lagrangiana? Novikov emula il tutto splittando in 2 particelle identiche.
Si, esatto. È ccomunque un esempio ipotetico, perché non viene in mente nessun modello realistico che sia in grado di generare una CTC di quel tipo (a meno di ricorrere allo spaziotempo di Gödel, ma in questo caso ritornerei al modello di Novikov).
Funzionerebbe in questo modo: ho una pallina che compie un moto unidimensionale ed è libera da forze. In uno spaziotempo piatto, percorrerebbe una retta (che possiamo assumere come asse x del sistema di riferimento inerziale da cui si osserva il moto). La linea di universo della particella è ovviamente una retta che giace all’interno del cono-luce.
E fino qui niente di nuovo.
Ora se immaginiamo uno spaziotempo curvo (non necessariamente dotato di CTC), vuol dire che siamo in presenza di un qualche corpo massivo che incurva lo spaziotempo, e magari si potrebbe considerare un qualche tipo di metrica particolare, come Schwartzschild o Kerr. E anche qui niente di nuovo, perchè tali spazi non ammettono CTC (almeno credo, forse in presenza di una singolarità si potrebbero generare).
Se invece consideriamo uno spaziotempo 2-dim che rappresentato dalla superficie di una sfera, le linee coordinate di tipo spazio sono archi di equatore, mentre le linee del tempo sono archi di meridiani. E questi ultimi sono curve chiuse, quindi CTC. Ne consegue che una qualunque pallina lanciata in questo spazio, prima o poi collide con se stessa “nel passato”, dando luogo al paradosso del nonno.
Bisognerebbe scrivere l’integrale d’azione, contenente ovviamente il determinante del tensore metrico, etc. etc., dopodichè annullarne la variazione prima (principio di minima d’azione), tirando fuori le equazioni del moto e vedere cosa effettivamente succede… Appena ho un pò di tempo ci provo…
Certo, ho inteso quello che vuoi dire. Ho ancora il dubbio di cosa tu intenda con spazio tempo 2-dim. Se intendi uno spazio tempo piatto (senza curvatura) di Minkowski, allora non puo’ essere modellizzato da una sfera S2 in alcun modo. Questo perche’ lo spazio tempo piatto implica che le coordinate vigano le trasformazioni di Lotentz, che implicano vincoli molto stretti fra le x e le t. Questi vincoli fanno si che se si vuole modellizzare questo spazio tempo con una superficie 2D immersa in uno spazio 3D, allora questa superficie non puo’ che essere che un iperboloide.
Se invece consideri anche spazi tempi curvi, con curvatura positiva, allora certamente puoi avere una sfera S2. Ma e’ impossibile muovere x e t come coordinate di longitudine e latitudine su una sfera, proprio perche’ sono legate dalle equazioni di Lorentz, che emulano una geometria iperbolica sottostante.
L’unico modo per modellizzare il tutto con una sfera, allora si potrebbe considerare una sfera di Riemann, proprio come fa Penrose sul suo libro sugli spinori/tensori. Ma chiaramente e’ un caso diverso, che richiederebbe coordinate complesse.
Volevo segnalare 2 libri sui wormholes molto interessanti, che ho preso tempo fa subito aver visto il film Insterstellar di Nolan (che consiglio, visto che il responsabile tecnico/scientifico e’ proprio Kip Thorne):
1) The Physics of Stargates. Parallel universes, Time Travel and the Enigma of Wormhole Physics. Molto bello, descrive sia i wormholes quantistici, che quelli classici (relativistici). C’e’ anche un capitolo che descrive come costruire un wormhole dal punto di vista ingegneristico.
2) Lorentzian Wormholes, from Einstein to Hawking. Un po’ piu’ tecnico di quello qui sopra, ma indicato anch’esso poiche’ affronta il tutto partendo dai lavori dei piu’ grandi della SR e GR.
@Ricccardo
Hai scritto nel commento: “Ho ancora il dubbio di cosa tu intenda con spazio tempo 2-dim. Se intendi uno spazio tempo piatto (senza curvatura) di Minkowski, allora non puo’ essere modellizzato da una sfera S2 ”
No, intendo uno spaziotempo curvo, cioè la superficie di una sfera. Precisamente, lo spazio fisico è 1-dimensionale, ma curvo. Aggiungendo la dimensione temporale (altrettanto curva) abbiamo uno spaziotempo curvo. Con una particolarità (inserita ad hoc): questo spaziotempo è dotato di CTC. Quindi le linee coordinate temporali devono chiudersi a loop. E qual è l’esempio più semplice e più maneggevole? Quello della sfera
Il mio dubbio era solo dato dal fatto che sopra parlavi di spazio tempo di Minkowski, che e’ appunto piatto. OK, grazie
Un altro modo di usare i wormholes per i viaggi nel tempo e’ quello costituito dal cosidetto Roman Ring:
https://en.wikipedia.org/wiki/Roman_ring
Nella gergo tecnico in uso, una macchina del tempo e’ tale se sposta la particella nel tempo e ma non nello spazio, ovvero se il DeltaX nella metrica e’ nullo. Questa, ad esempio, e’ l’uso che viene fatto di 1 wormhole nei 2 articoli citati qui sopra, dove il wormhole e’ considerato puntiforme tant’e’ che la particella rischia (ma poi abbiamo visto che la “fisica” evita che questo accada, almeno nei calcoli) di ritrovarsi indietro nel tempo a interagire con se stessa, quindi in un intorno opportuno dello stesso punto.
Nel 1997, Visser (che e’ anche l’autore del secondo libro che ho suggerito, Lorentzian WormHoles) propose a Thorne una configurazione diversa, mettendo in anello diversi wormholes, dove per anello si intende un anello nello spazio-tempo. In pratica qui ogni wormhole non funziona come una macchina del tempo, poiche’ oltre che spostare nel tempo sposta anche nello spazio. Per intenderci, 1 di questi wormholes potrebbe spostare avanti di 1000 anni partendo dalla Terra e uscendo su Canopus (pianeta molto caro a Wheeler in tutti i suoi libri di SR/GR), ad esempio. Ecco, concatenando N wormholes di questo tipo, ovvero facendo in modo che il wormhole 2 abbia l’entrata nello spazio-tempo vicino all’uscita del wormhole 1 e cosi’ via, si puo’ teoricamente far si che l’ultimo wormhole abbia l’uscita vicino (dove per vicino si intende un intorno topologico in tutto lo spazio-tempo) all’entrata del primo wormhole. In questo modo il tutto e’ equivalente a un unico wormhole che fa viaggiare SOLO nel tempo, cioe’ una macchina del tempo, appunto.
Cmq, sutdi piu’ approfonditi hanno messo in rilievo che una configurazione di “macchine” di questo tipo tende ad andare in risonanza, sperimentando un “positive feedback” che disrompe l’anello di Roman in tempo zero. Questo viene visto come un effetto della chronology conjecture protection, postulata appunto da Hawking, che vieta a oggetti simili di formarsi.
Correggo alcune inesattezze che ho scritto ieri: il determinante della metrica (in valore assoluto e sotto radice quadrata) interviene se si considera la densità di lagrangiana, e infatti sqrt(|g|)d^4x, individua l'”elemento di volume” dello spaziotempo.
Il modellino giocattolo di uno spaziotempo 2-dim sferico è del tutto irrealistico. Ho ripescato un vecchio testo di Relatività Generale dove è trattata la metrica di Gödel in maniera più soft del testo di Hawking, e mi voglio togliere lo sfizio di tirar fuori qualcosa…..
Spinto dalla curiosita’ del 2-Dim sferico da te proposto, che trovo molto intrigante, ho provato a cercare, o perlomeno immaginarmi, una distribuzione di massa (anche solo 1-D) che possa generare una metrica di quel tipo. Non ci sono riuscito (con questo non voglio dire che non esista, anzi sarei interessatissimo a vederne un esempio).
Per il resto, anch’io ieri sera ho aperto il testo di Hawking sulla metrica di Godel, ed e’ effettivamente 1 po’ (tanto) tricky. L’approccio di Novikov non mi sembra male cmq. Ancora non mi faccio persuaso che si possa modellizzare 1 wormhole in un modo cosi’ “semplice”.
Novikov considera uno spazio fisico 3-dim. per ovvie ragioni: innanzitutto è necessario considerare l’interazione gravitazionale che “plasma” la struttura a larga scala dell’universo. Quindi è costretto a riferirsi a un biliardo 3-dim., anche se poi la logica impone un biliardo 2-dim come il biliardo di Sinai, giusto per fare un esempio matematico. In ogni caso, un biliardo è 2dim e le biglie si muovono su tale superficie.
Nel caso della sfera S (che poi potremmo considerare di raggio unitario, quindi S2) si potrebbe aggiungere una dimensione spaziale realizzando un biliardo a tutti gli effetti (ipersfera). Ma secondo me è preferibile considerare S2. C’è comunque una perplessità. Adottando le usuali coordinate sferiche (theta,phi) dove la prima svolge il ruolo di coordinata di tipo tempo, si può scrivere il tensore metrico che risulta diagonale in quanto le linee coordinate sono ortogonali. Sul libro di Landau (teoria dei campi) c’è un’argomentazione molto chiara sulla sincronizzazione degli orologi in RG. Una condizione necessaria e sufficiente è che deve essere g_0k=0 cicoè le componenti tempo-spazio del tensore metrico devono annullarsi. In tal caso il corrispondente sistema di riferimento in cui è scritta la metrica, risulta essere “sincrono”, e ci dà la possibilità di definire un “tempo universale”. Ed è quello che succede con la metrica di Friedman-Robertson-Walker, in conseguenza del principio cosmologico (isotropia e omogeneità dello spazio fisica “per ogni istante di tempo universale”).
Nel caso di uno spaziotempo sferico 2-dim. il tensore metrico risulta diagonale, per cui a più forte ragione, il sistema di coordinate (theta,phi) risulta essere sincrono. E al contempo ammette CTC, giacché le linee coordinate temporali sono meridiani, ovvero curve chiuse. Qui c’è una contraddizione perché affinché esista una CTC non deve esserci un “tempo universale” per cui le componenti tempo-spazio del tensore metrico devono essere non nulle. E invece nel caso della sfera S2 ciò non accade. In altre parole, abbiamo un sistema di coordinate sincrono che ammette CTC.
Gödel “molto furbamente” fece in modo da tirar fuori una metrica con componenti tempo-spazio non nulle, in modo da rendere impossibile una sincronizzazione e, quindi, l’esistenza di un tempo universale. Infatti, lo scopo supremo di Gödel (da buon platonico) era quello di fare piazza pulita del tempo!
Pensandoci cmq meglio, sarebbe stato bello che uno spazio-tempo cosi’ semplice come una S2 potesse contenere CTC. Immagino cmq che, se fosse stato possibile, un genio come Godel (e annessi) non si sarebbe messo a congetturare un universo rotante cosi’ complesso come quello che ha fatto.
Pensandoci bene, non mi vengono in mente metriche diverse da quella di Godel che ammettano CTC. Non mi e’ nemmeno chiaro quale metrica abbia usato Navikov per modernizzare il suo wormhole (visto che non mi pare la si citi nel documento).
Francamente non ho letto l’articolo di Novikov, giusto per non farmi condizionare. Ne ero a conoscenza per poi scaricarlo da internet, in seguito alla lettura di un articolo del cosmologo F. De Felice che citava Novikov e il suo prinicipio di autoconsistenza.
Riguardo allo spaziotempo 2-dimensionale sferico: ripensandoci, non può esistere uno spaziotempo del genere (anche generalizzando a 4 dim) perché tutte le linee coordinate temporali sono CTC, per cui ogni particella collide con sé stessa nel passato. In altre parole, in un tale spaziotempo il principio di causalità è ampiamente violato.
Ho riletto entrambi i pdf e posso confermare che Novikov modellizza il wormhole tipo black box, semplicemente applicando il principio di minima azione senza nemmeno scomodare la relativita’.
La semplicita’ (vista da fuori) con cui inchioda le traiettorie self-consistent, scartando le altre, e’ veramente impressionante.
Concordo sicuramente con Godel e col suo tentativo, anche non sono ne saro’ lontamente paragonabile a una mente del genere. Come ho gia’ avuto modo di dire, concordo al 100% con Rovelli e col suo approccio privo di tempo. Il tempo non e’ nulla che si possa misurare direttamente, ma solo mediante il muoversi reciproco di altre cose (lancette, onde, etc).
Ma non divaghiamo.
Quello che hai descritto ha perfettamente senso e puo’ solo implicare una cosa (per quel che vedo): non si puo’ usare uno spazio-tempo sferico e avere CTC allo stesso tempo. Quindi, non solo la sfera S2 non e’ realistica, ma non va proprio bene insieme alle CTC.
Se guardi infatti a pag 169 del libro di Hawking, si vede che le sue CTC sono si wrappano su un iperboloide, cioe’ sul classico “embedded diagram” che si vede in giro rappresentante 1 buco nero o metriche simili,
Io credo che, benché per noi sia innaturale, lavorare con un iperboloide e’ molto piu’ realistico che con una sfera. D’altro canto un universo AdS (Anti de Sitter) e’ proprio quello utilizzato col principio oleografico ed ha massima simmetria con curvatura negativa.
@Ricccardo
“Ho riletto entrambi i pdf e posso confermare che Novikov modellizza il wormhole tipo black box, semplicemente applicando il principio di minima azione senza nemmeno scomodare la relativita’.
La semplicita’ (vista da fuori) con cui inchioda le traiettorie self-consistent, scartando le altre, e’ veramente impressionante.”
Stupefacente! Un risultato indipendente dalla metrica e dal paradigma (relativistico o newtoniano) è praticamente universale. Ciò è corroborato dal fatto che il principio di minima azione è a tutti gli effetti, un principio primo della fisica. Mi
Mi sa che dovrò leggere con attenzione gli articoli…
Infatti stavo pensando proprio alla stessa cosa, ovvero un risultato indipendente dalla metrica. Probabilmente e’ proprio per quello che questo principio e praticamente accettato da tutti, poiche’ necessita’ proprio solo del principio di minima azione come assunto base. Sarei proprio contento se riuscissi a leggerli anche tu (io li ho letti non in modo approfondito, ovvero per ora solo per capirne le basi e il filo conduttore, non ho quindi seguito e verificato nel dettaglio tutti i passaggi) in questo modo potrei avere un tuo parere (anche tecnico) su entrambi. Se posso, ti consiglio di leggerli nell’ordine in cui me li hai mandati (ovvero con quello del biliardo per ultimo) anche se il primo e’ piu’ lungo del secondo, ma secondo me introduce meglio il principio che poi verra’ usato nel successivo (infatti l’ordine di tempo con cui sono stati scritti e anche l’ordine con cui me li hai passati).
Grazie ancora.
inizierò a leggerli in ordine cronologico. C’è quello del 1996 sul principio di autoconsistenza, seguito da quello sul biliardo.
L’unico assunto sulla metrica che posso vedere, nel primo articolo, e’:
“Moreover, spacetime outside the ‘time machine’ is approximated to be Minkowskian, and the motion of the particle to be non-relativistic.”
Quindi non dice nulla sulla metrica interna al wormhole, ma solo sull’esterna, appunto piatta.
@Riccardo. Prima di leggere l’articolo, sto cercando di capire meglio la fisica che c’è dietro http://www.extrabyte.info/2017/11/22/giocando-una-partita-al-biliardo-di-novikov/
OK, grazie della notifica. Credevo che il caso S2 fosse stato escluso, ma vedo che cmq lo citi nel tuo articolo. Per una persona che non abbia seguito questo scambio e che legga direttamente l’articolo, credo possa un po’ fuorviante, visto che non descrive nulla di effettivamente realistico, ne rappresenta una struttura causale, come da te scritto sopra. Oltre a questo, hai tu stesso dimostrato che uno spazio-tempo S2 non possa contenere CTC, proprio perche’ ha le componenti spazio-tempo nulle.
In ogni caso, come detto, non credo possa esistere una fisica piu’ semplice di quella descritta da Navikov. E’ inutile impegolarsi con metriche, basta supporre che con lo spazio-tempo sia piatto fuori dal wormhole.
Lo so, però voglio almeno togliermi lo sfizio di calcolare le componenti del tensore energia-impulso della “materia” che genera quel tipo di metrica.
Certamente Marcello, ci mancherebbe, non voleva essere una critica. Consideravo solo l’ipotesi di scrivere nell’articolo del blog gli stessi dubbi che e conclusioni che hai postato qui, cosi’ da dare all’avventore occasionale il quadro.
Per il resto, il calcolo che ti appresti a fare e’ sicuramente interessante, per lo meno da un punto di vista squisitamente matematico di geometria differenziale.
diciamo che il post del blog è solo una bozza o meglio, ne seguiranno altri, spero più definitivi. ps. Rimane stimolante l’idea della black box. Personalmente la vedo come un sistema che accetta in input un istante t2, per poi restituire un istante t1<t2. In tal modo viene generata una discontinuità di prima specie della funzione che esprime il tempo in funzione dell'ascissa (sempre nel caso 1-dim) della biglia. Spero di quantificare al meglio al più presto
“però voglio almeno togliermi lo sfizio di calcolare le componenti del tensore energia-impulso della “materia” che genera quel tipo di metrica.”
Questo e’ sicuramente interessante. Come ti ho detto in un post qui sopra, non riesco proprio a immaginarmi quale distribuzione di materia-energia (che poi e’ la stessa cosa, chiaramente) possa generare una metrica 1-D diffeomorfa a S2. Molto interessante sicuramente.
riguardo alla discontinuità della linea di universo, intendevo una cosa tipo questa http://extrabyte.info/biliardo_novikov002.pdf
Si certo, mi pare sensato se si considera il wormhole come black box.
Quindi quello che ti accingi a fare e’: considerata la metrica diagonale (tensore 2 X 2 con componenti miste nulle) vai prima a calcolare il tensore di Ricci Ruv (l’ho scritto in forma completamente coartante, porta pazienza non ho un’equazione editor qui), da questo contrarre al Ricci scalar R e poi componendo questi con la metrica vai a ottenere il left hand side delle famose equazioni di Einstein. Una volta calcolato questo, vai a a ricavare il right hand side che contiene il tensore Tuv. Giusto?
Stavo cmq guardando il tuo diagramma con la discontinuità. E’ sicuramente giusto dal punto di vista di un osservatore stazionario col wormhole. Pensavo cmq che solitamente sullo stesso grafico si mette anche il punto di vista dell’oggetto in moto (chiaramente si puo’ rovesciare il tutto, considerando ferma la particella e muovendo il wormhole, ma teniamo il primo punto di vista).
Come anche indicato da Novikov, la palla da biliardo vede il wormhole come puntiforme (non perche’ si muova a velocità’ relativistiche e quindi si contragga, bensi’ perche’ la “puntiformita’” del wormhole e’ un assunto dell’articolo) ma cmq lo attraversa senza discontinuità’ (proprio come avviene per un osservatore che attraversi l’orizzonte degli eventi di un buco nero, che non si accorge di averlo passato, poiche’ la metrica e’ ancora piatta in quel punto).
Mi chiedevo quindi se sia corretto sovrapporre i 2 punti di vista, avendo 2 diagrammi che non sarebbe topolgicamente equivalenti, poiche’ uno e’ discontinuo e l’altro no.
Non ho mai visto diagrammi spazio-tempo discontinui, da cui la mia curiosita’ e la mia domanda.
Hai scritto:”Quindi quello che ti accingi a fare e’: considerata la metrica diagonale (tensore 2 X 2 con componenti miste nulle) vai prima a calcolare il tensore di Ricci Ruv (l’ho scritto in forma completamente coartante, porta pazienza non ho un’equazione editor qui), da questo contrarre al Ricci scalar R e poi componendo questi con la metrica vai a ottenere il left hand side delle famose equazioni di Einstein. Una volta calcolato questo, vai a a ricavare il right hand side che contiene il tensore Tuv. Giusto?”
Esatto. Faccio l’opposto di quello che si fa solitamente
Riguardo all’altro commmento:
Si, ho capito a cosa ti riferisci (se ho ben inteso), cioè inserire anche gli assi coordinati (t’,x’) che definiscono il sistema di riferimento solidale alla particella. Cmq ho provato con un ragionamento molto semplice, considerando solo il sistema di riferimento inerziale K da cui si osserva il moto della particella. Immaginiamo che questa sia effettivamente una palla di biliardo, che viene lanciata da un giocatore G che poi osserva il moto. All’istante t2 la palla entra nel wormhole (che possiamo anche noi assumere puntiforme). Nota: a t2 l’ascissa della particella è x2. “Istantaneamente” (il wormhole è fermo rispetto a K) il wormhole shifta il tempo a t1<t2. Dal momento che lo shift è istantaneo, avrà ancora ascissa x2 (cioè quella che aveva a t1). Conclusione: all'istante t1 è come se la particella avesse due ascisse diverse. Il paradosso generato dalla discontinuità sta nel fatto che G vede all'istante t1 "due palline", in quanto la seconda è quella con il tempo shiftato.
Non so se è giusto tutto questo…
Si, hai ben inteso, volevo infatti dire sovrapporre allo stesso diagramma anche l’altro punto di vista (e questo solitamente si fa appunto sovrapponendo degli assi inclinati x’ e t’, inclinati in funzione del solito coefficiente beta). Io credo che quello che dici sia corretto, anche se “atipico”. E lo dico suffragandolo con l’approccio di Novikov: sembra proprio che per evitare questo paradosso, Novikov abbia introdotto il trucco delle 2 particelle identiche. In questo modo ha preso 2 piccioni con una fava: ha evitato discontinuità e paradossi come quello qui sopra, ma soprattutto ha permesso di modellizzare l’interazione della pallina nel passato con 2 palline al posto di una. E’ sicuramente un modo molto complicato (ma anche molto semplice ed efficace allo stesso tempo) di realizzare le cose. Ma puo’ darsi che Novikov fosse abituato a lavorare con questi concetti e quindi gli fosse piu’ naturale splittare gli attori in questo modo.
e allora mi sa che dovrò leggermi seriamente l’articolo di Novikov. Fino ad ora abbiamo giocato con le palle da biliardo 😀
sto leggendo l’articolo, e mi sembra di aver capito che la seconda biglia è, in realtà, la “versione futura” della prima. Quindi, in sostanza Novikov non si sorprende più di tanto. Ho dato un’occhiata al saggio “la quarta dimensione” dello scrittore (e matematico) Rudy Rucker. Di seguito un paio di foto del libro:
http://www.extrabyte.info/rucker_book1.jpg
per guardare la seconda, cambia 1 in 2 nel link sopra (se posto il secondo link, il filtro antispam del blog mette il commento nella coda di moderazione).
Stavo pensando di affrontare il problema dal punto di vista della geometria differenziale, nel senso che anziché modellizzare una TM attraverso un sistema I/O, si potrebbe schematizzare mediante un “generatore di sostituzioni di parametro non ammissibili”. Infatti, lo shift temporale può essere interpretato come una riparametrizzazione della traiettoria della pallina. Ma questa parametrizzazione non è per niente regolare, e come ben si sa, le situazioni matematicamente patologiche mal si adattano alla fisica.
Si, il trucco delle biglie fa si che a un certo punto la versione passata e futura coesistano, dove il verbo coesistere presume una simultaneita’ che viene misurata nel sistema solidale al wormhole.
Quindi ci sono “realmente” 2 palline, ovvero la stessa pallina torna nel passato e il principio di self-consistency vieta che questa pallina del passato cozzi col suo futuro. Ma non vieta nulla che ci siano 2 palline, la presente e la futura, ad un dato momento. Il fatto di considerare paradossale 2 versioni di noi stessi e’ solo un problema nostro mentale, per cui non riusciamo ad accettare questa cosa. In realta’ il principio di autoconsistenza non vieta questa cosa, vieta solo che la particella del passato possa interagire con se stessa nel futuro.
Messa in quel modo, la particella 2 non andrà mai in collisione con la particella 1, in quanto la particella si sposta. Questo viene riportato anche nel libro di Rucker
Esattamente, infatti il senso e’ proprio quello. Il principio di self-consistenct afferma che le traiettorie possibile sono tali per cui c’e’ una “censorship” naturale che evita che la particella dal passato cozzi nel futuro, in modo da innescare paradossi.
Io la immagino cosi’, facendo finta che l’attore sia io: sono nel futuro, attraverso il wormhole e finisco nel passato. Ecco dal quel momento ci saranno 2 me, ma nessuno dei 2 sara’ a conoscenza dell’altro, poiche’ la fisica e’ tale che non ci incontreremo mai. E quando dico: “incontreremo” intendo che non potremo MAI scambiarci informazioni, ovvero uno non sapra’ mai dell’esistenza dell’altro, poiche’ le traiettorie spazio-temporali saranno nettamente “lontane” nello spazio tempo.
Pero’ mi chiedo, andando oltre: l’esperimento mentale di Novikov prevede che la palla torni indietro in un passato ed eviti se stessa. Questo quindi, come detto sopra, vale anche per un “me stesso”. Mi chiedo pero’: come fa la sua modellizzazione a evitare che io torni indietro PRIMA della mia nascita, evitando che io uccida mia madre?
Non c’e’ traccia (credo) in nessuno dei documenti una situazione in cui la palla compaia in un passato prima che la sua versione vecchia fosse gia’ presente presso il wormhole.
Mi spiego meglio:la pallina esce dal wormhole in un passato dove essa stessa NON E’ ancora entrata nel wormhole. Il tempo passa e a un certo punto la sua versione nel passato arriva davanti al wormhole e si ritrova la sua copia dal futuro. Come e’ possibile evitare la collisione in quel caso?
Probabilmente le traiettorie vietate di Novikov sono tali da essere nello spazio tempo, quindi anche quella situazione dovrebbe essere gestita (anche se non l’ho vista nel documento).
Alcune osservazioni al volo: secondo me non c’è bisogno di invocare la Relatività Ristretta, va bene anche l’approccio newtoniano. Infatti, Novikov contempla una palla di biliardo che “per forza di cose” è un oggetto non relativistico, per cui Newton calza a pennello 😀 . D’altra parte, anche Rucker considera la relatività, ma solo per considerare le linee di universo. Però i diagrammi del tipo spaziotempo vanno bene anche in ambito non relativistico. Si tratta appunto dei “diagrammi orari”, come si vede da qui
http://extrabyte.info/grafici_novikov000.jpg
e quindi la pallina 2 collide con la pallina 1 se e solo se la pallina 1 è in quiete. Penso comunque che sia piuttosto fastidiosa la presenza di due versioni distinte dello stesso oggetto nel medesimo istante (istante misurato nello stesso sistema inerziale) sia pure spazialmente separati (sempre rispetto allo stesso sistema inerziali da cui si osserva il moto). Forse bisogna invocare la Many Worlds Interpretation di Everett: ogni oggetto shiftato nel tempo è automaticamente splittato in un altro spaziotempo.
Infatti non mi pare di aver tirato in mezzo la relativita’ speciale, ho solo detto che l’articolo di Novikov suppone che l’esterno del WH sia piatto, in modo da poter applicare la fisica newtowniana.
Un altro modo di risolvere e’ infatti la many worlds. come ho gia’ avuto modo di dirti, io non sono d’accordo con quel punto di vista. Lo trovo completamente un trucco per sfuggire alle spiegazioni piu’ dritte. Non capisco come tirar in ballo mondi che poi cmq non possono scambiare informazione fra di loro possa avere una qualsiasi rilevanza fisica (non e’ un critica a te, ci mancherebbe).
Per me non c’e’ nessun problema ad accettare che ci siano 2 istanze di me in un dato momento. Anche la fisica ammette questa cosa, e’ solo paradossale per la nostra visione del mondo.
E infatti, tutta la spiegazione di Novikov si basa sulla coesistenza di 2 particelle che sono la stessa particella nel passato/futuro.
Mi spiego meglio, perche’ sono sicuramente concetti complessi (forse i piu’ complessi e dibattuti della SR/GR). Come ho detto non ho problemi ad accettare 2 versioni della stessa pallina allo stesso istante (nello stesso sistema inerziale). Neanche Novikov ha infatti problemi ad accettarlo e a modellizzarlo. La cosa veramente importante e’ che queste 2 palline non possano interagire in alcuna forma. Se e’ cosi’ veramente (come sembrerebbe dal principio di self-consistency) allora non sono legate da alcun che e possono coesistere. Chiaramente e’ ancora piu’ difficile accettare che 2 versioni di un essere senziente possano coesistere, ma anche qui e’ solo una questione mentale da accettare. Se io nel passato non so che sto convivendo con un me stesso dal futuro, poiche’ non posso interagire con lui (e non posso saperlo, visto che l’evento nel futuro non e’ ancora accaduto dal mio punto di vista) allora e come se l’altro me non esistesse, e quindi posso convivere senza paradossi.
Contemporaneamente consideriamo il me senziente che arriva dal futuro: in questo caso io so che sto tornando indietro nel tempo, ma quando arrivo non trovo un altro me nel passato perche’ non posso cmq interagire con lui. Quindi, da un certo punto di vista, e’ come se ci fossero 2 mondi che convivono ma senza vedersi. Questo pero’ non vuol esattamente dire che sono mondi appartenenti alla teoria dei molti mondi. Sono mondi che si fondono nello stesso spazio-tempo con linee di universo che non si incontreranno mai.
Da qui, per tornare al mio primo post sopra, considerando 1 essere senziente il principio di Novikov implica che questo essere non possa avere libero arbitrio (free will) quando si tratti di viaggi indietro nel tempo.
Proprio come la pallina non ha modo di scegliere la propria traiettoria quando esce nel passato, allora nemmeno un senziente potra’ farlo.
Questo e’ un passo enorme, poiche’ implica appunto che il free will non si possa applicare ai viaggi nel passato: la “natura” sa cosa e’ meglio e come influenzare le linee di universo di oggetti provenienti dal futuro in modo che non ci sia interazione.
sono d’accordo su tutta la linea, in particolare su ciò che hai scritto nell’ultimo commento:
“Proprio come la pallina non ha modo di scegliere la propria traiettoria quando esce nel passato, allora nemmeno un senziente potra’ farlo.”
In sostanza, la pallina ha memoria del proprio stato iniziale, e in virtù del determinismo fisico (valido, visto che siamo a scala macroscopica) non è libera di modificare il proprio stato meccanico appena uscita dalla time machine…
Si esattamente Marcello. Questo e’ quello che ho capito sinora da questo principio. Ho cmq pensato a lungo alla spiegazione a molti mondi. Effettivamente, come detto sopra, anche nella spiegazione “normale”, la pallina esce nel passato e non puo’ avere alcuno scambio informativo con la sua versione nel passato (e viceversa, ovviamente). Quindi e’ come se ci fossero 2 mondi che non si possono parlare. C’e’ pero’ appunto un enorme differenza per me: la teoria a molti mondi prevede che ogni mondo abbia il suo spazio-tempo, mentre la versione “normale” di Novikov prevede che le 2 palline coesistano nello stesso spazio-tempo, anche senza interazione.
Personalmente, io sono per il rasoio di Occam ovunque sia applicabile, per cui vedo l’ipotesi dei molti mondi come un “di piu’ non necessario”, visto che il tutto e’ gia’ spiegato nella versione di Novikov SENZA avere paradossi.
Detto questo, mi sono ripromesso di stampare il primo articolo, quello del 96, e rileggerlo a fondo cercando di capire il piu’ possibile.
Perfetto. A me nel frattempo sono venute alcune idee su ciò che cchiamerei “moti cinematicamente possibili”, nel senso che definire il tempo t come una funzione dell’ascissa x (al contrario di quello che si fa in cinematica newtoniana con i classici diagrammi orari x=x(t)) implica ovviamente che la funzione x(t) sia invertibile. In questo modo utilizzando alcuni teoremi di Analisi sull’invertibilità globale/locale, si arriva a capire che per creare un comportamento “patologico” del tipo Macchina del tempo, non c’è bisogno di avere una discontinuità. Quest’ultima si verifica solo se la scala dei tempi della Macchina è istantanea rispetto alla scala dei tempi del moto della particella.
ps. Nel frattempo, ieri sera, in un mercatino ho trovato per caso una copia di questo
http://www.fantascienza.com/catalogo/opere/NILF1068231/il-tempo-vuole-uno-scheletro/
A detta di Asimov, è un ottimo racconto sui viaggi nel tempo…..
Sembra interessante…anche a me piace moltissimo girare i mercatini.
Concordo sulla istantaneita’, infatti e’ proprio quell’assunto che genera il salto, ma Novikov non sembra preoccuparsene, poiche’ tanto il suo scopo e’ quello di scrivere l’integrale di azione su vari tempi in gioco e quindi, dal punto di vista dell’integrazione non ci sono problemi ad avere salti nel dt.
ho letto l’articolo di novikov ma fino a un certo punto, poi si complica con le varie condizioni. Probabilmente perchè nel caso di un urto elastico nello spazio, ci sono un tot di grandezze che non si possono determinare, nel senso che i principi di conservazione (quantità di moto ed energia cinetica) non bastano…
ho utilizzato il sistema del centro di massa e della coordinata relativa. Se ho fatto bene i conti è uscita fuori una condizione necessaria e sufficiente che utilizza il momento angolare della massa ridotta del sistema delle due palline http://www.extrabyte.info/time_machine_1dim.pdf
aggiungo: sarebbe interessante portare tutto a livello quantistico. Qui abbiamo un’onda di probabilità che si propaga deterministicamente, per cui dovrebbe spuntare Novikov
@Marcello, scusa il ritardo con cui ti scrivo, ma e’ un periodo di intenso lavoro che spesso mi lascia la sera in formato larvale (quando ancora peggio non mi porto a casa i grafi di visibilità’, diagrammi di Voronoi o altre diavolerie simili che uso al lavoro).
Ho visto che hai scritto una bella analisi e mi sono ripromesso di stamparla e leggerla nelle vacanze di Natale. Per quanto riguarda il “porting” quantistico del principio di Novikov, credo che sia una cosa molto complicata, anche solo da impostare. Tutta la dimostrazione “classica” di Novikov si basa sull’impiego di un potenziale “di contatto” (urto puntuale) fra le palle. Ecco, ovviamente questo urto puntuale non ha senso in QM, proprio per il principio di indeterminazione di Heisemberg, che impedisce di conoscere la posizione e la velocità’ di 1 particella (e quindi anche di 2 che interagiscono) con precisione arbitraria.
Quindi, un potenziale di contatto come quello classico non credo possa essere usato. Chiaramente si tratta di un problema di “scattering”, dove si devono impiegare altri potenziali piu’ usati un QM (buca di potenziale, well potential e simili). Senza contare il tirare in giorno l’effetto tunnel in QM, che per l’appunto buca i potenziali. Prima di tutto si tratterebbe gia’ di capire se le 2 particelle siano modellizzate come pacchetto d’onde (tipo Gaussiana) con velocità’ di gruppo data, oppure come equiprobabili su tutto lo spazio (quello che il buon Cesare Rossetti chiamava “normalizzazione in una scatola”.
Oltre a questo, se si entra nel regime di QFT, si tratta poi di capire se si parli di particelle bosniache, che quindi possono coesistere nello stesso stato, o fermiohiche, quindi sottoposte alla statistica di Fermi (e al principio di Pauli).
okk, considera che nel file pdf che ho linkato ci sono un tot di errori, anzi mi sono dimenticato di cancellare parte dell’appendice, cmq vedrò di aggiornarlo, soprattutto in vista del porting quantistico 🙂
Ho riletto il mio commento sopra, scusa per gli N refusi che vedo solo ora.
Purtroppo il correttore a volte e’ un po’ troppo invasivo.
Cmq devo ammettere che le particelle “bosniache” non sono poi cosi’ male come alternativa ai bosoni :-). A presto.
tranquillo, tanto in questi giorni sono in “stand by” con tosse+raffreddore, causa un imbecille che mi ha mischiato
Volevo anche segnalare questo bellissimo libro appena uscito e che attendevo da tempo:
https://www.amazon.it/gp/product/3319646109/ref=ox_sc_sfl_title_2?ie=UTF8&psc=1&smid=A11IL2PNWYJU7H
E’ di Peter Soit l’autore di Not Even Wrong (libro molto orientato contro le stringhe), dal quale ha anche tratto il blog omonimo:
http://www.math.columbia.edu/~woit/wordpress/
Il libro suddetto descrive molto bene, partendo da zero, tutta la parte di Lie Group/Lie Algebra non dando per scontato nulla, e arrivando a descrivere molto bene il Modello Standard.
Un bel regalo di Natale che mi concederò 🙂
Sorry, I really meant “Peter Woit” 🙂