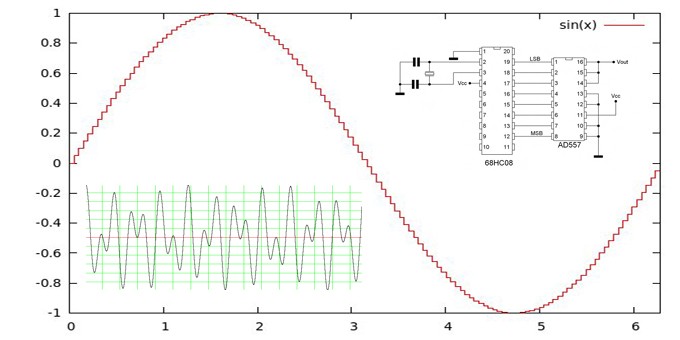
Una tecnica per generare forme d’onda sinusoidali ad elevata precisione a partire da una serie di valori costanti predefiniti e memorizzati nella memoria del microcontrollore ed inviati ad un convertitore DA. La generazione di sinusoidi risulta particolarmente utile nell’uso del DTMF, nella generazione di toni singoli o per la realizzazione di generatori di segnale.

LA TECNICA DI SINTESI ARITMETICA

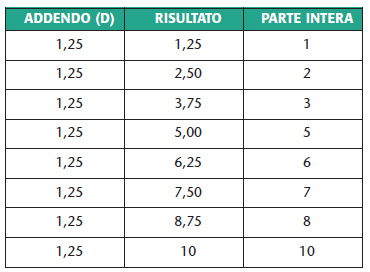
La tecnica illustrata in questo articolo è nota come Sintesi Aritmetica in quanto prevede la creazione di una tabella (detta tabella di look-up) di valori corrispondenti all’ampiezza della sinusoide in determinati istanti di tempo. Questa si contrappone alla tecnica di Sintesi Digitale Diretta in cui la distanza temporale tra due valori della tabella di look-up è costante. Come esempio verrà considerata un tabella con 256 entrate. La tecnica prevede che il prelevamento di un campione  della sinusoide dalla tabella di  look-up avvenga indirettamente  attraverso una costante D costituita da una parte intera e da una parte decimale e rappresentata da due byte: il byte più significativo è la parte intera, mentre quello meno significativo è la parte frazionaria. L’entrata della tabella da cui verrà prelevato il campione è data dalla parte intera della somma ripetuta della costante D con se stessa. Ad esempio se D=1,25  sommando  ripetutamente 1,25 si ottiene la seguente sequenza di valori:

L’effetto della presenza di una parte frazionaria nella costante D, si ripercuote nel risultato provocando un salto occasionale di  valore (nell’esempio mancano infatti i valori 4 e 9 nella parte intera del risultato). È possibile dunque  determinare la parte intera e la parte frazionaria della costante D affinché la sinusoide di uscita abbia una frequenza ben definita. Per una tabella a 256 entrate la relazione per il calcolo della costante D è la seguente:

D=256 x F x S

dove F è la frequenza desiderata per l’onda in uscita e S è il periodo di prelevamento del campione ed è dato da: S=(1/FCLK)x Nc dove FCLK  è la frequenza di un ciclo istruzione ed Nc  il numero di cicli istruzione in un loop. Ecco un esempio numerico. Un microcontrollore  operante ad 8MHz esegue una routine da 29 cicli istruzione per generare una sinusoide di 8KHz utilizzando una tabella da 256 entrate. Per quanto già visto di ha:

S = 125nsec x 29 = 3,625 µsec

La costante D vale quindi:

D=256 x 8000 [Hz] x 3,625 [µsec] = 7,424

Dunque la parte intera vale 7 (il byte più significativo vale 0x07) e la parte frazionaria vale 0,424 (il byte meno significativo vale 0x6C ovvero 0,424 x 256).

Effetti collaterali: phase jitter

La tecnica di sintesi aritmetica, pur consentendo la generazione di sinusoidi di frequenza ben precisa, produce alcuni effetti che ne escludono l’uso in alcune applicazioni. L’effetto preponderante è il cosiddetto rumore di fase altrettanto noto come phase jitter. In una sinusoide pura il periodo è costante ad ogni ciclo per cui la frequenza istantanea del segnale coincide sempre con la frequenza media. Generando una sinusoide con la tecnica appena descritta, la frequenza istantanea cambia da periodo a periodo a causa del salto occasionale del valore intero già descritto in precedenza anche se la frequenza media dell’onda rimane costante e stabile. Per questo motivo l’onda generata con un algoritmo di sintesi aritmetica non è adatta in applicazioni in cui la frequenza istantanea deve essere costante o dove  non  sono ammesse componenti  armoniche diverse dalla fondamentale.

IMPLEMENTAZIONE HARDWARE

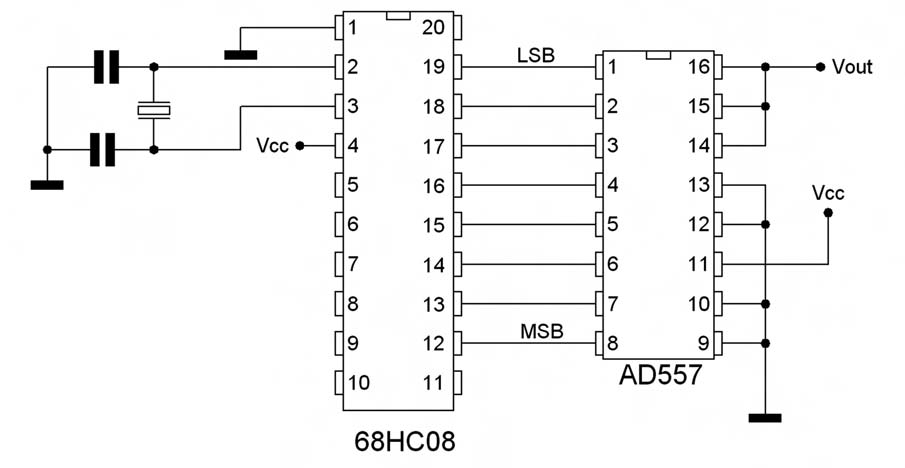
Come esempio pratico di sintesi aritmetica, verrà illustrato un progetto impiegante un microcontrollore HC08 di Freescale collegato con un convertitore digitale-analogico AD557 di Analog Devices come mostrato in figura 1.

Figura 1. Schema elettrico per la generazione di una sinusoide mediante sintesi aritmetica

Il microcontrollore  utilizza l’algoritmo di sintesi aritmetica per prelevare dalla tabella di look-up i valori di ampiezza della sinusoide (ciascuno espresso su un byte) che provvede ad inviare al convertitore. Quest’ultimo è collegato in modo da essere sempre attivo operando così una conversione continua del segnale digitale. La continuità della conversione è garantita dalla connessione a massa dei segnali /CS e /CE del convertitore.

IMPLEMENTAZIONE FIRMWARE

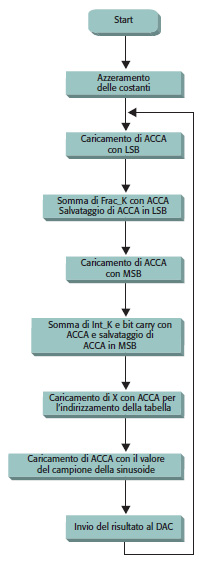
La figura 2 mostra il diagramma di flusso del programma  per  la generazione dell’onda.

Figura 2. Diagramma di flusso della routine di generazione della sinusoide

Tale programma implementa l’esempio precedentemente esaminato per generare una sinusoide da 8KHz. Il listato 1 riporta integralmente  la routine  in assembler.  Int_K e Frac_K sono rispettivamente le parti intera e frazionaria della costante D calcolate nell’esempio precedente e valgono Int_K=0x07 e Frac_K=0x6C. La routine prevede 29 cicli istruzione per cui se intendete modificarla sarà opportuno ricalcolare il valore della costante D in funzione del nuovo numero di cicli istruzione. Ovviamente è possibile inserire uno stadio amplificatore in uscita al DAC in modo da poter variare l'ampiezza della sinusoide e adattare l'impedenza di uscita per il pilotaggio di carichi a bassa impedenza di ingresso. La routine riportata nel listato 1 è scritta in assembler e può  essere compilata  direttamente nell’ambiente CodeWarriorTM, il tools per lo sviluppo di applicazioni con i microcontrollori  Freescale.

PortA equ $01
DAC equ PortA;porta a cui è collegato il DAC
ORG $50
AccumLSB       RMB 1
AccumMSB       RMB 1
Frac_K         RMB 1
Int_K          RMB 1
ORG $6E00
START          EQU *
ArithSyn       clr AccumLSB
clr AccumMSB
SignalGen      lda AccumLSB
add Frac_K
sta AccumLSB
lda AccumMSB
adc Int_K
sta AccumMSB
tax
lda SineTable,X
sta DAC
bra SignalGen
**********************Tabella dei campioni della sinusoide**************************
SineTable      FCB $80,$83,$86,$89,$8C,$90,$93,$96
               FCB $99,$9C,$9F,$A2,$A5,$A8,$AB
               FCB $AE,$B1,$B3,$B6,$B9,$BC,$BF,$C1
               FCB $C4,$C7,$C9,$CC,$CE,$D1,$D3
               FCB $D5,$D8,$DA,$DC,$DE,$E0,$E2,$E4
               FCB $E6,$E8,$EA,$EB,$ED,$EF,$F0
               FCB $F1,$F3,$F4,$F5,$F6,$F8,$F9,$FA
               FCB $FA,$FB,$FC,$FD,$FD,$FE,$FE
               FCB $FE,$FF,$FF,$FF,$FF,$FF,$FF,$FF
               FCB $FE,$FE,$FE,$FD,$FD,$FC,$FB
               FCB $FA,$FA,$F9,$F8,$F6,$F5,$F4,$F3
               FCB $F1,$F0,$EF,$ED,$EB,$EA,$E8
               FCB $E6,$E4,$E2,$E0,$DE,$DC,$DA,$D8
               FCB $D5,$D3,$D1,$CE,$CC,$C9,$C7
               FCB $C4,$C1,$BF,$BC,$B9,$B6,$B3,$B1
               FCB $AE,$AB,$A8,$A5,$A2,$9F,$9C
               FCB $99,$96,$93,$90,$8C,$89,$86,$83
               FCB $80,$7D,$7A,$77,$74,$70,$6D
               FCB $6A,$67,$64,$61,$5E,$5B,$58,$55
               FCB $52,$4F,$4D,$4A,$47,$44,$41
               FCB $3F,$3C,$39,$37,$34,$32,$2F,$2D
               FCB $2B,$28,$26,$24,$22,$20,$1E
               FCB $1C,$1A,$18,$16,$15,$13,$11,$10
               FCB $0F,$0D,$0C,$0B,$0A,$08,$07
               FCB $06,$06,$05,$04,$03,$03,$02,$02
               FCB $02,$01,$01,$01,$01,$01,$01
               FCB $01,$02,$02,$02,$03,$03,$04,$05
               FCB $06,$06,$07,$08,$0A,$0B,$0C
               FCB $0D,$0F,$10,$11,$13,$15,$16,$18
               FCB $1A,$1C,$1E,$20,$22,$24,$26
               FCB $28,$2B,$2D,$2F,$32,$34,$37,$39
               FCB $3C,$3F,$41,$44,$47,$4A,$4D
               FCB $4F,$52,$55,$58,$5B,$5E,$61,$64
               FCB $67,$6A,$6D,$70,$74,$77,$7A,$7D
ORG $FFFE
DW START

Ti potrebbe interessare anche:

Fast Fourier Transformation: riconosciamo un DTMF

Generatore DTMF con micro RENESAS

Generatore di funzioni DDS fino a 10 MHz