In moltissime applicazioni, dal consumer all’industria alle più avanzate funzioni del medicale, si utilizza come riferimento per l’automazione ed il controllo il PID, ossia un particolare algoritmo di controllo che consente di avere rapidità di azionamento, assenza di errore a regime e controllo sulla variazione dei segnali.
Introduzione analitica
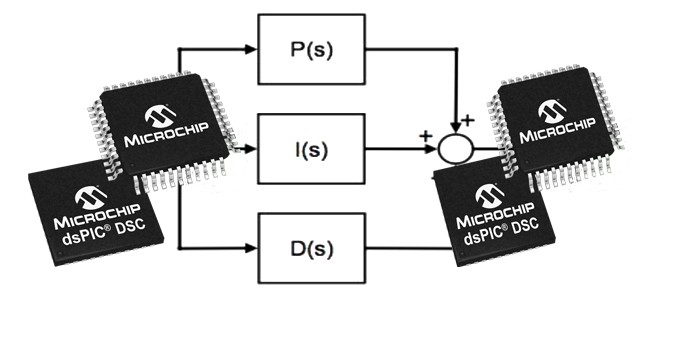
PID è l’acronimo che sta ad identificare le parole Proporzionale, Integrale e Derivativo. Questi tre aggettivi identificano tre diverse tipologie di algoritmi che consentono di osservare e controllare un qualsiasi sistema di azionamento. Innanzitutto, per poter comprendere cosa sia e come agisca un PID, bisogna avere una rappresentazione analitica del sistema da controllare. Solo in questo modo sarà possibile realizzare un studio analitico che consenta di ottimizzare il controllo già “sulla carta”. In assenza di una rappresentazione analitica del sistema, saranno le sole prove empiriche a poter garantire delle performance ottimali per il nostro controllo. Si consideri il sistema da controllare caratterizzato da una Funzione di Trasferimento P(s). Come si vede la variabile in gioco è “s”, che significa che si sta operando nello spazio delle trasformate di Laplace, utilizzate per caratterizzare un sistema per il suo comportamento in frequenza. Se consideriamo U(s) quale ingresso del sistema e Y(s) l’uscita, possiamo inserire nel controllo un blocco chiamato R(s), che è appunto il controllore PID. Come si vede, si è considerato un ingresso costante nel tempo U/s, che consente di alleggerire la trattazione matematica. Con riferimento alla figura 1.
si può vedere che l’ingresso del blocco PID è costituito dalla differenza fra ingresso del sistema ed uscita del sistema, ossia dall’errore. Il blocco in retroazione 1/k rappresenta un coefficiente moltiplicativo che costituisce il trasduttore dell’uscita. La funzione additiva Z(s), infine, costituisce il rumore che inevitabilmente si introduce fra l’uscita del PID e il sistema da controllare. La funzione matematica dell’uscita nel dominio di Laplace è quella riportata in figura 2.
La W(s) è appunto la funzione di trasferimento del PID, che ingloba la R(s), e gli effetti che questo blocco ha sul sistema P(s). A titolo di esempio, andiamo a studiare un sistema da controllare la cui funzione di trasferimento sia asintoticamente stabile. Una funzione di trasferimento si dice asintoticamente stabile quando essa non converge ad un valore, ma oscilla all’infinito attorno a questo valore senza mai centrarlo. In figura 3 una immagine esemplificativa di risposta ad un ingresso a gradino unitario da parte di un sistema di questo tipo (nell’ipotesi che il valore dell’uscita a regime debba essere pari ad 1).
Controllore P:
Come detto, il sistema di controllo PID è costituito da tre componenti. La componente proporzionale consiste in pratica nella semplice moltiplicazione dell’errore per un opportuno coefficiente, chiamato Kp (si ricorda che l’errore è la differenza fra ingresso e uscita del sistema). Questa componente garantisce al sistema una banda passante più elevata, quindi una maggior reattività alle variazioni. Oltre a questo la componente proporzionale rende il sistema più immune ai disturbi e alle variazioni parametriche, dal momento che “esalta” il solo valore della differenza fra ingresso ed uscita. Il suo difetto è che la stabilità del sistema può risultare diminuita, dal momento che il controllo può uscire dai margini di stabilità. Oltre a questo, non si garantisce al sistema l’annullamento dell’errore a regime, ossia non è detto che il sistema “centri” il valore desiderato per l’uscita Y(s). La W(s) nel caso di un controllo proporzionale sarà quella di figura 4.
Nell’esempio del sistema precedente, l’applicazione di un controllo proporzionale pari a Kp=9 ha l’effetto di smorzare le oscillazioni a regime, di rendere molto più rapido l’assestamento dell’uscita attorno al valore finale, di ridurre di molto la massima sovraelongazione, ossia il rapporto fra il massimo valore e il valore desiderato. Il problema che si riscontra è nel valore cui si assesta l’uscita, ossia 0,8, diverso dal desiderato 1. In figura 5 l’andamento dell’uscita in risposta al gradino, del sistema così modificato.
Controllore PI:
Il controllore PI aggiunge alla funzione proporzionale la funzione integrativa. Quest’ultima, come accennato, annulla del tutto gli effetti dei disturbi e delle variazioni parametriche sull’uscita del sistema. Ciò significa che la parte più consistente della correzione è a carico della parte proporzionale, mentre la parte di raffinazione è affidata alla parte integrale. Chiaramente, questo significa che se il valore desiderato per l’uscita è 1, quest’ultimo sarà raggiunto senza errore grazie agli effetti del controllore PI. Di contro, però, la banda passante del sistema e, di conseguenza, i margini di fase del sistema controllato sono ridotti di 90°, a causa dell’azione ritardatrice dell’operatore matematico integrale Ki/s. In figura 6 la funzione di trasferimento di un controllore PI.
Nell’esempio del sistema preso in esame precedentemente, l’effetto di una costante proporzionale Kp pari a 8,1 e di una costante integrativa Ki pari a 4,76, è la totale correzione dell’errore a regime (si noti che il valore raggiunto dall’uscita a regime è pari ad 1 come mostra la figura 7).
La velocità del sistema, però, rimane sempre abbastanza limitata, dal momento che il segnale risulta assestato entro l5% dal valore di regime in 7-8 secondi.
Controllore PD:
Il controllore PD unisce alle già citate funzionalità garantite dal termine proporzionale la capacità di “prevedere” l’andamento dell’errore garantita dal termine derivativo. Quest’ultimo, infatti, analizza la differenza fra l’errore del tempo T-1 e quello del tempo attuale, andando a correggere a seconda che questa differenza sia crescente o decrescente. I vantaggi del termine derivativo corrispondono ad un miglioramento di 90° del margine di stabilità, grazie all’effetto anticipatore del termine Kd*s. Questo corrisponde anche ad una riduzione della massima sovraelongazione e del tempo di assestamento, garantendo quindi un miglior andamento dell’uscita ed uno stress ridotto a carico del sistema controllato. Di contro, però, il termine derivativo enfatizza gli effetti delle componenti ad alta frequenza, compreso dunque il rumore. Proprio per questa sua caratteristica, il controllore PD non viene mai utilizzato quasi mai. In figura 8 gli effetti di un controllore PD sul sistema in esame. La costante proporzionale Kp vale 9 e la costante derivativa Kd vale 3,6.
Come si può notare, rimane la presenza di un errore a regime, dal momento che il valore raggiunto è 0,8. Di contro, però, si ha una sovraelongazione pressoché nulla e un tempo di assestamento inferiore a 5 secondi, con un miglioramento del 40% rispetto ai casi precedenti.
Controllore PID:
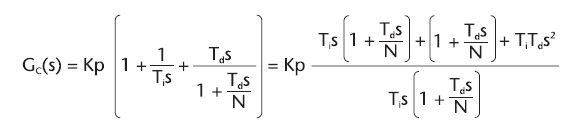
Il controllore PID unisce i pregi dei controllori precedentemente analizzati e, grazie all’effetto di cancellazione dei poli-zeri che si ottiene dalla combinazione delle componenti integrale e derivativa, realizza un contenimento degli effetti “indesiderati” citati in precedenza. Nella pratica, il PID è il sistema di controllo utilizzato nella stragrande maggioranza dei casi. Il sistema controllato presenta debole sovraelongazione, tempo di assestamento abbastanza contenuto, grazie anche alle scarse oscillazioni del segnale in uscita, oltre che assenza di errore a regime. In figura 9 la funzione di trasferimento.
In figura 10 la risposta del sistema, con un controllo proporzionale con costanti pari a Kp=10,8, Kd=2,7 e Ki=10,8.
Il PID in un dsPIC Microchip
Passando dall’analisi matematica al mondo pratico, è possibile implementare un controllore PID operante in real time su un sistema fisico, come ad esempio un motore, utilizzando un microcontrollore dotato di una potenza di calcolo medio alta. È questo il caso dei dsPIC30F e dei dsPIC33F di Microchip, che grazie alla capacità di eseguire la MAC (Multiply And Accumulate) in un unico ciclo macchina, sono in grado di gestire i complessi calcoli che stanno dietro alla analisi matematica di un PID senza perdere in efficienza. Ragionando dunque su un sistema fisico quale un motore Brushless in corrente continua dotato di sensori di Hall per il rilevamento della velocità, la rappresentazione a blocchi del sistema può essere quello di figura 11.
Come si vede, il Set Point è costituito dalla velocità desiderata per il motore, che in un caso pratico potrebbe essere ottenuta da un potenziometro, o da un pedale. Questo valore viene poi sottratto alla velocità attuale del motore, grazie al calcolo di velocità operato dal dsPIC che legge tramite gli ADC i sensori di Hall posti sul motore stesso. Questa differenza di velocità costituisce appunto la grandezza standard di ingresso per un PID, ossia l’errore. Questo errore viene trasformato dal PID in una tensione, che è la grandezza con cui vengono pilotati gli avvolgimenti del motore stesso, con l’obiettivo di correggere l’errore fino ad annullarlo. Andando ad “aprire” il blocchetto PID, si può suddividere il suo funzionamento in tre diverse componenti, che sono per l’appunto le tre diverse caratteristiche analizzate in precedenza dal punto di vista analitico (figura 12).
La trasformata di Laplace utilizzata nell’analisi matematica, è caratterizzata da una variabile s che, come visto, è tempo continua. Nel microcontrollore chiaramente una variabile di questo tipo non è rappresentabile, per cui gli analitici hanno realizzato una variabile tempo discreta, “z”, tramite la quale si possono controllare le grandezze in esame senza perdere in sensibilità, a patto che gli slot temporali siano sufficientemente piccoli (ecco perché si richiede un microcontrollore di elevata potenza). In figura 13 sono riportati i singoli componenti del PID nello spazio delle trasformate Z.
Similmente a quanto visto nella trasformata di Laplace, si individua la componente di ritardo di fase presente nel termine integrale e quella di anticipo di fase presente nel termine derivativo. Queste due componenti utilizzano il termine z-1, che corrisponde ad un quanto temporale. La somma dei tre termini sopra riportati conduce, dopo semplici passaggi matematici, al risultato di figura 14.
Si tratta dunque di una combinazione di somme e prodotti che, come detto, sono facilmente implementabili in un dsPIC. La possibilità di realizzare una somma ed un prodotto in un unico ciclo macchina, per giunta, rende ancor più snella la gestione di questa operazione analitica, consentendo la possibilità di gestire segnali che variano assai rapidamente nel tempo.
Il PID a livello macchina
Ecco dunque cosa accade, a livello logico, all’interno del dsPIC. Come si vede dalla figura 15, un potenziometro esterno fissa il Set Point di velocità, nel caso di questo esempio.
Segue poi lo schema visto in precedenza, con il PID che analizza la grandezza “errore” e genera delle tensioni di riferimento per il generatore Motor Control PWM (rif. Articolo di Maurizio Del Corso, Firmware n.2). Dal motore torna un feedback dai sensori di Hall, che grazie alla caratteristica del Timer1 di esser sensibile al cambiamento di fronte (Change Notification), dà una informazione sulla posizione angolare del motore in un dato momento. Oltre a questo, grazie agli Input Capture, si può ricavare il calcolo della velocità, necessario a ricostruire la grandezza Errore per l’ingresso PID. La grandezza “Velocità Misurata” è calcolata come il rapporto fra il minimo periodo misurato e il periodo effettivo di base dell’Input Capture. Questo calcolo, com’è chiaro, deve avvenire in tempi rapidissimi, dal momento che alcuni motori (trapani per dentista, controlli per la robotica) viaggiano a velocità angolari superiori ai 10.000 giri al minuto. Nel listato 1 si riportano alcune porzioni di firmware, scritto in C per il compilatore Microchip C30.
void __attribute__((__interrupt__)) _T1Interrupt (void)
{
IFS0bits.T1IF = 0;
Period = ActualCapture - PastCapture; //Unsigned substraction
if (Period < (unsigned int)MINPERIOD) // MINPERIOD = 6000 rpm
Period = MINPERIOD;
else if (Period > (unsigned int)MAXPERIOD) // MAXPERIOD = 60 rpm
Period = MAXPERIOD;
// This sub in assembly calculates the Speed using fractional division
// MINPERIOD
// Speed = (Fractional divide) ---------------
// Period
SpeedCalculation();
SpeedAbsValue = Speed;
// Speed sign adjustment based on current motor direction of rotation
if (Current_Direction == CCW)
Speed = -Speed;
// Condition RPM SFRAC16 SINT HEX
// Max Speed CW -> 6000 RPM -> 0.996805 -> 32663 -> 0x7F97
// Min Speed CW -> 60 RPM -> 0.009984 -> 327 -> 0x0147
// Min Speed CCW -> -60 RPM -> -0.009984 -> -327 -> 0xFEB9
// Max Speed CCW -> -6000 RPM -> -0.996805 -> -32663 -> 0x8069
// Speed PID controller is called here. It will use Speed, RefSpeed, Some
// buffers and will generate the new voltage for the SVM.
SpeedControl();
// Set minimum ControlOutput to 10% to keep the motor running
if (ControlOutput < 3276)
ControlOutput = 3276;
MotorStalledCounter++; // This variable is cleared in halls ISRs
if ((MotorStalledCounter % _10MILLISEC) == 0)
{
ForceCommutation();
//Force Comm. if no hall sensor changes have occured in specified timeout.
}
else if (MotorStalledCounter >= _100MILLISEC)
{
StopMotor();
// Stop motor is no hall changes have occured in specified timeout
}
return;
}
_SpeedCalculation:
MOV __MINPERIOD, W8
MOV _Period, W9
REPEAT #17
DIVF W8, W9
MOV W0, _Speed
RETURN
_SpeedControl:
BSET CORCON, #SATA ; Enable Saturation on Acc A
; Init Pointers
MOV #_ControlDifference, W8
MOV #_PIDCoefficients, W10
MOV #_RefSpeed, W1
MOV #_Speed, W2
MOV #_ControlOutput, W0
; Calculate most recent error with saturation, no limit checking required
LAC [W1], A
LAC [W2], B
SUB A
SAC A, [W8]
; Prepare MAC Operands
MOVSAC A, [W8]+=2, W4, [W10]+=2, W5
LAC [W0], A ; Load Acc with last output
; Perform MAC
REPEAT #2 ; Repeat 3 times
MAC W4*W5, A, [W8]+=2, W4, [W10]+=2, W5
; Store result in ControlOutput with saturation
SAC A, [W0]
BCLR CORCON, #SATA ; Disable Saturation on Acc A
MOV #_ControlDifference, W8
MOV [W8+2], W2 ;ControlDifference[2] = ControlDifference[1]
MOV W2, [W8+4]
MOV [W8], W2 ;ControlDifference[1] = ControlDifference[0]
MOV W2, [W8+2]
RETURN;
La prima porzione di firmware consente di recepire l’informazione nei pin impostati come Input Capture e di analizzarne i contenuti: si notino in particolare la limitazione della rotazione al range [60…6000] giri al minuto, il calcolo di velocità dal Input Capture, la gestione della Force Commutation se il PID non recepisce variazioni dai sensori di Hall e per finire la procedura di controllo della velocità, cioè del PID vero e proprio. Sia la “Speed Calculation” che la “Speed Control” sono scritte in Assembly, al fine di ridurre quanto più possibile il tempo di esecuzione del calcolo della velocità e di esecuzione del PID.


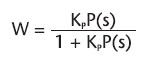
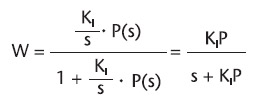
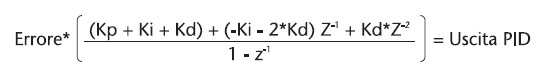



Il pid che dal punto di vista teorico potrebbe essere semplice, in pratica non lo e’ affatto. Matlab permette di fare simulazioni varie e creare il codice C da implementarlo successivamente in qualche micro. In ambito industriale semplici regolatori standard consistono nel variare alcuni parametri per il sistema in questione.
Lineare e semplice, ma anche sufficientemente dettagliato. Complimenti, bella trattazione.